https://arxiv.org/abs/2501.04304
Abstract
Text-to-Image 생성을 위한 Diffusion모델은 높은 계산량과 메모리사용으로 인해 실제 적용에 제약을 줌.
이를 하기 위해 Quantization 기법이 이용되는데, 기존 Diffusion모델의 quantization은 낮은 비트에서 이미지 품질과 텍스트-이미지 alignment를 유지하는데 한계를 지님.
본 논문에서는 activation에서 outlier가 있으며, 이는 이미지 품질을 결정하는데 중요한 역할을 한다는 것을 분석함. 또한, 텍스트-이미지 alignment에 cross-attention이 중요한 역할을 한다는 것을 분석함.
논문에서 제안하는 DGQ(Distribution-aware Group Quantization)는 Pixel-wise와 Channel-wise 간 균형을 맞추기 위한 Group-wise quantization 기법을 활용하며, 텍스트-이미지 alignment 성능을 유지하기 위해 <Start> token을 제외한 token들에 대해 logarithmic quantization scaling 방식을 채택함.
DGQ는 MS-COCO와 PartiPrompts 데이터셋에서 실험되었으며, 추가적인 fine-tuning이나 weight quantization을 진행하지 않고도 low-bit환경에서의 text-to-image diffusion 모델을 성공적으로 quantize 함.
Introduction
Text-to-Image 생성에서 Diffusion Model이 매우 활발히 쓰이고 있음. 하지만 높은 자원사용량으로 인해 자원이 제약되는 장치나 실시간 적용에는 한계를 보임.

이를 해결하기 위해 model quantization이라는 방식이 많은 주목을 받고 있으며, diffusion 모델에도 quantization은 활발히 적용되고 있음.
하지만, 많은 기존의 quantization 방식들은 text-image alignment를 유지하는데 어려움을 겪음. 이는 생성형모델에서 매우 중요한 요소이나 간과되고 있음.
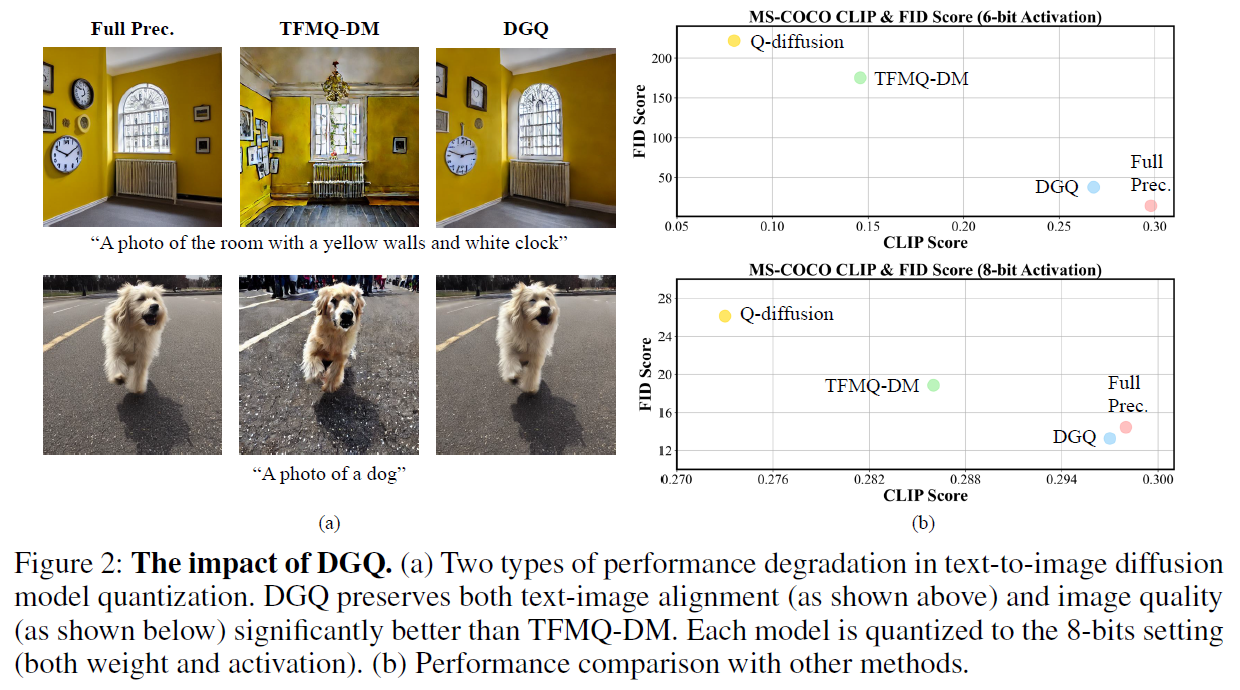
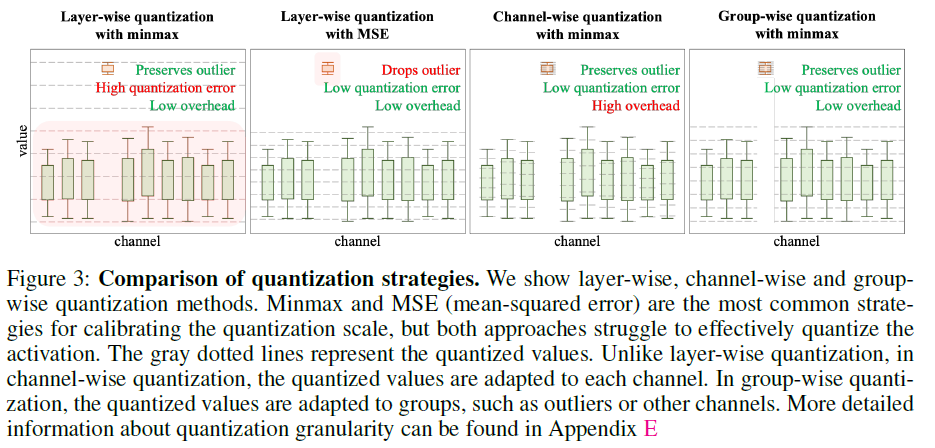
Figure3에서는 Layer-wise와 Channel-wise 간 특성과 장단점에 대해 설명함.
Layer-wise Quantization에서 minmax의 경우 outlier에 대해서는 보존 가능하나 scaling 범위가 커져 quantization error(quantization granularity 떨어짐)가 커지는 것을 확인할 수 있음. MSE의 경우는 granularity를 보장하여 quantization error는 적지만 outlier를 처리하지 못한다는 한계가 존재함.
Channel-wise Quantization의 경우 outlier도 보존하고 quantization error도 보장하지만, overhead가 매우 높기 때문에 이에 대한 대안으로 DGQ에서는 group-wise quantization 방식을 최종적으로 활용함.
본 논문에서는 low-bit환경에서도 하드웨어 친화적인 text-to-image diffusion quantization 방식을 제안하며, 높은 이미지 퀄리티를 보장하면서도 우수한 text-image alingment를 보장함.
저자들은 quantization 과정에서 성능을 보장하기 위한 key characteristic을 다음과 같이 제시함.
C1) Activation에서는 Outlier가 존재하며, 이는 이미지 퀄리티에 중요한 영향을 미침. 또한, layer-wise quantization은 outlier에 대응하지 못하여 성능저하가 두드러짐. C2)Stable Diffusion에 쓰이는 Cross-Attention은 Self-Attention과 달리 <Start> 토큰에서 매우 큰 값이 attention 됨. 기존의 uniform quantizer로는 <Start> 토큰 외 다른 작은 값들이 무시되어 text-image alignment를 심각하게 저하시킴
이를 바탕으로 저자들은 C1을 해결하기 위해 Group-wise Quantization을 하였으며, C2를 해결하기 위해 <Start> 토큰을 quantization에서 제외함.
Contributions
1) Text-to-Image Diffusion에서의 activation에는 Cross-Attention이 독특한 패턴을 가지며, 이는 기존의 quantization 방식으로는 성능저하가 이뤄짐을 식별
2) Start Token Activation의 Outlier를 보존하는 DGQ (Distribution-aware Group Quantization)을 제안함.
3) GDQ는 low-bit 환경에서 좋은 이미지 퀄리티를 보장하며, 높은 text-image fidelity를 보임.
4) MS-COCO 데이터셋에서 좋은 성능을 보이며, fine-tuning 없이 low-bit quantization을 가능하게 함.
Method
Text-to-Image Diffusion Model 특성 분석
Quantization을 효과적으로 하기 위해 Text-to-Image Diffusion 모델의 특성을 저자들은 먼저 분석함
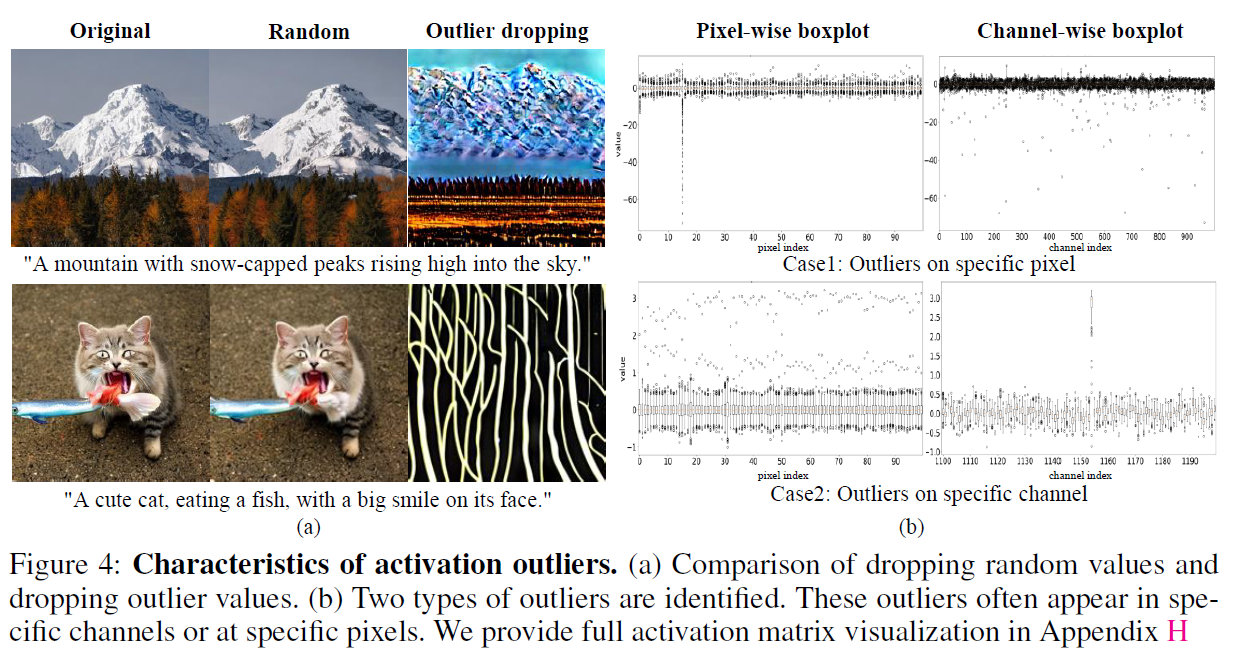
Figure 4의 (a)에서 'original'은 원본, 'random'은 random한 하나의 activation을 제거한 경우이며, 'outlier dropping'은 outlier activation을 제거한 경우임. 실험결과 outlier는 이미지 퀄리티에 상당한 영향을 미침을 알 수 있음.
Figure 4의 (b)에서는 어떤 layer에서는 pixel별로 outlier가 나타나며, 어떤 layer에서는 channel별로 outlier가 나타남을 확인함. 또한, 이러한 현상은 seed나 prompt가 바뀌어도 지속적으로 나타나는 특징이며, stable diffusion의 고유 특성임을 확인함.
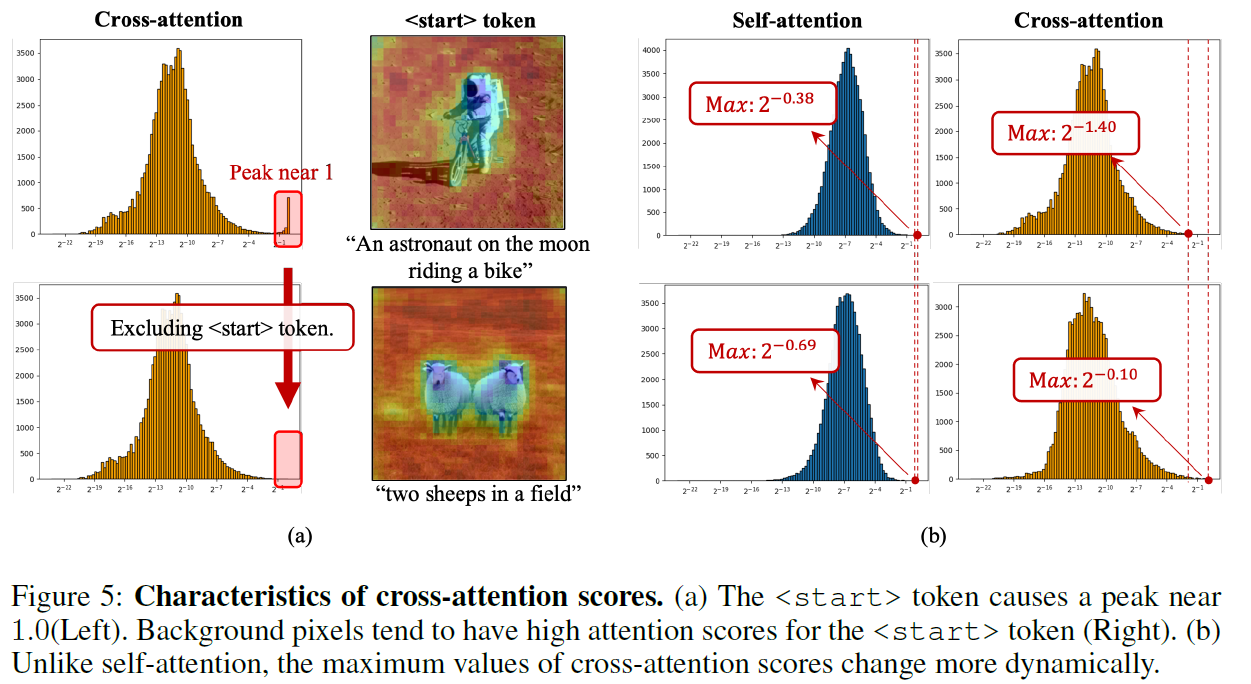
이는 Cross-Attention을 하는 과정에서 <Start> 토큰의 값이 두드러지게 나타남.
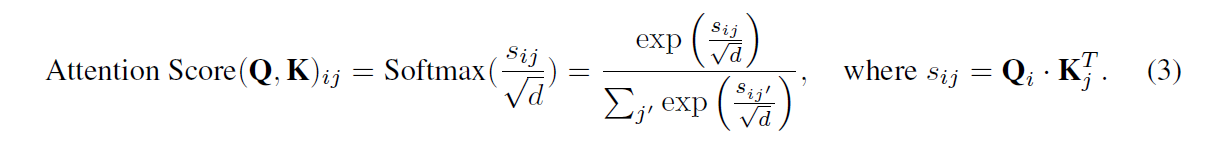
수식 3에서 보이는 것과 같이 attention score는 로그 스케일을 사용함.
Self-Attention에서는 q와 k가 가우시안 분포를 따르며, attention score 또한 가우시안 분포에 가깝게 형성됨. (Figure 5의 b)
반면 Stable Diffusion에서 사용하는 Cross-attention의 경우 <start> 토큰 때문에 peak가 존재하며 <bos> 토큰에도 피크가 존재함을 저자들은 확인함. 따라서 Cross-Attention에서는 Self-Attention과 달리 score의 최댓값 및 분산이 크게 흔들리며, 분포 또한 매우 크게 변동됨. (Figure 5의 b)
Distribution-Aware Group Quantization
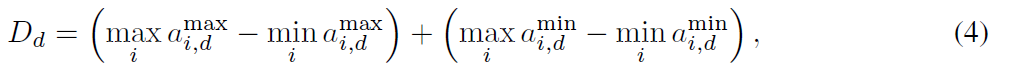
수식 4는 각 dimension에 대한 activation value들에 대한 variability를 측정하는 지표임. 각 $a$는 $i$번째 vector에 대한 최댓값과 최솟값을 의미하며 이 수식은 channel과 pixel dimension마다 달라지는 activation range의 차이를 표현할 수 있음.
Optimal 한 dimension을 찾기 위해 다음과 같은 수식을 활용함. 여기서 $d^*$은 $D_d$가 가장 큰 값이 선정되었을 때 그 값을 grouping에 활용하기 위해 사용됨.
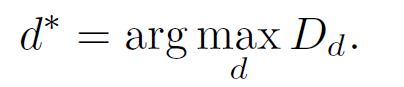
Optimal한 $d^*$를 찾았을 때, 아래와 같이 activation value들을 $K$ group으로 나누어 scaling factor $S$와 zero-point $z$를 구함.
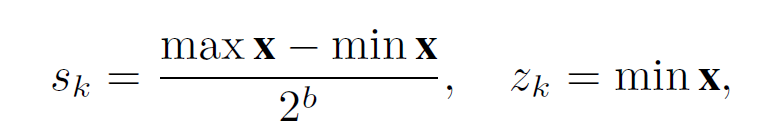
각 layer에 대한 최종적인 scaling factor들과 zero-point는 아래와 같이 구성됨.
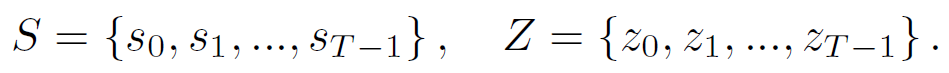
Attention-Aware Quantization
Cross-Attention은 주로 linear quantization(Uniform quantization)을 적용하는데 이러한 방식들은 위에서 기술했듯이 outlier 분포를 보존하지 못해 성능이 저하되는 문제가 발생함.
이를 해결하기 위해 cross-attetion과 self-attention 모두에 logarithmic quantization을 적용하여 기존의 quantization방식으로는 보존할 수 없던 작은 값들을 log scale에서 보존함.
또한 Cross-attention에서 <start> 토큰은 quantization을 진행하지 않고 full-precision에서 수행함.
(Softmax 연산은 보통 full-precision에서 수행되기 때문에 추가적인 dequantization이 필요하지 않아 하드웨어 구현 효율성이 높음)
마지막으로, cross-attention은 input prompt에 따라 분포의 변동이 크기 때문에, dynamic quantization을 적용하여 <start>토큰을 제외한 score 최댓값을 기반으로 프롬프트별로 scaling 함.
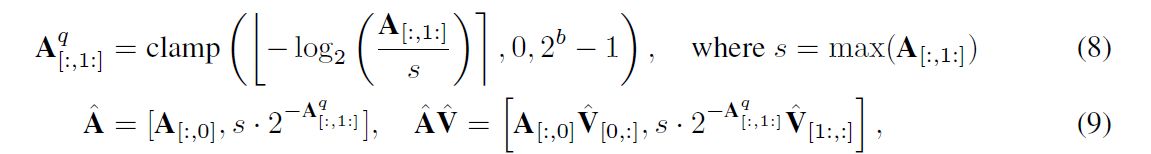
$\hat{A} \in \mathbb{R}^{n_q \times n_k}$ 는 quantized attention score이며, $\hat{V} \in \mathbb{R}^{n_v \times d}$ 는 quantized value를 의미함.
또한, 수식 8에서 $A$는 full-precision attention score를 의미하며, $n$은 각각 query, key, value에 대한 token 개수를 나타냄.
Experiments
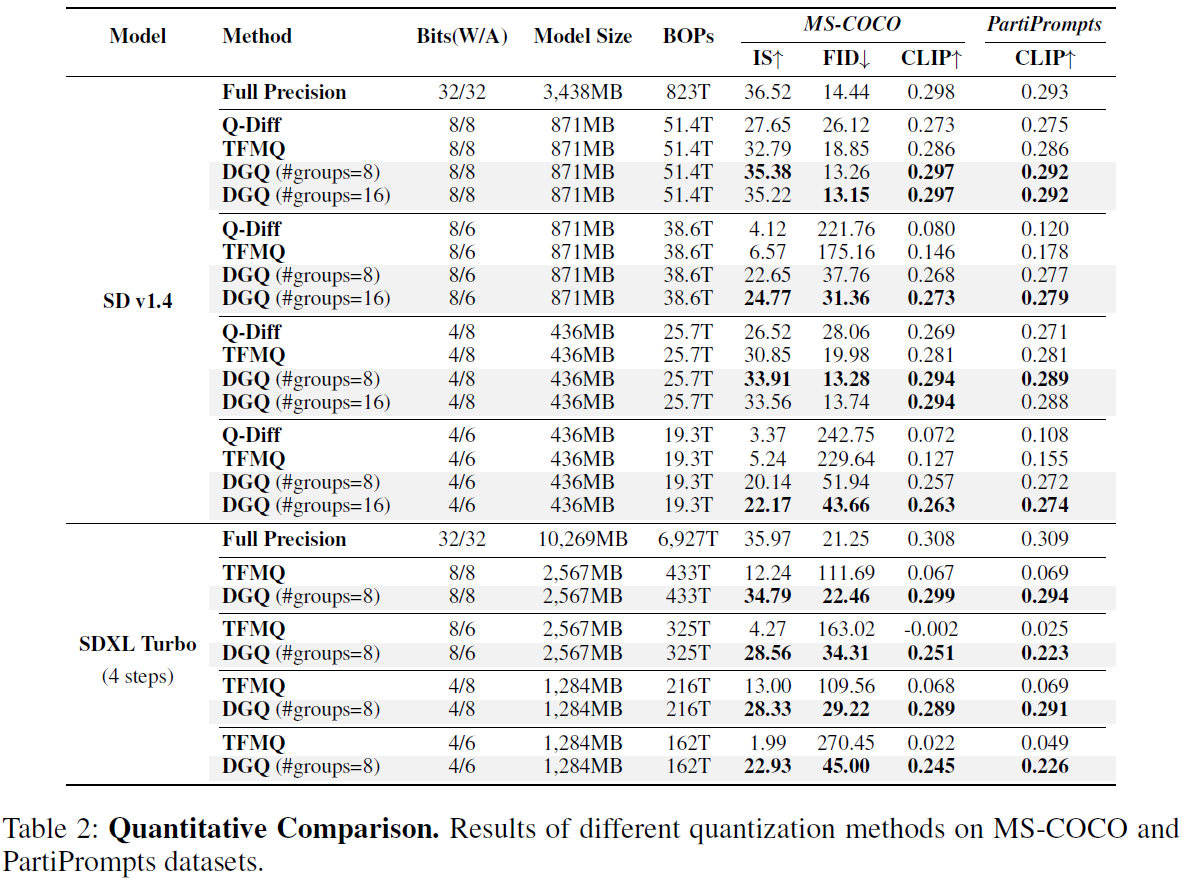
실험은 Q-diffusion과 TFMQ-DM을 baseline으로 진행하였으며, weight quantization의 경우 BRECQ와 Adaround를 기반으로 수행됨.
prompt로는 MS-COCO 데이터셋에서 64개의 caption을 뽑아서 사용하였음. 모델로는 Stable Diffusion v1.4와 SDXL Turbo를 사용하였고, group-size는 8과 16을 활용하였음. DGQ가 모든 baseline에 비해 SOTA성능을 보임. 정성적 평가에서도 다음 Figure와 같이 우수한 생성능력을 보임.

Ablation Study는 다음과 같이 진행함.
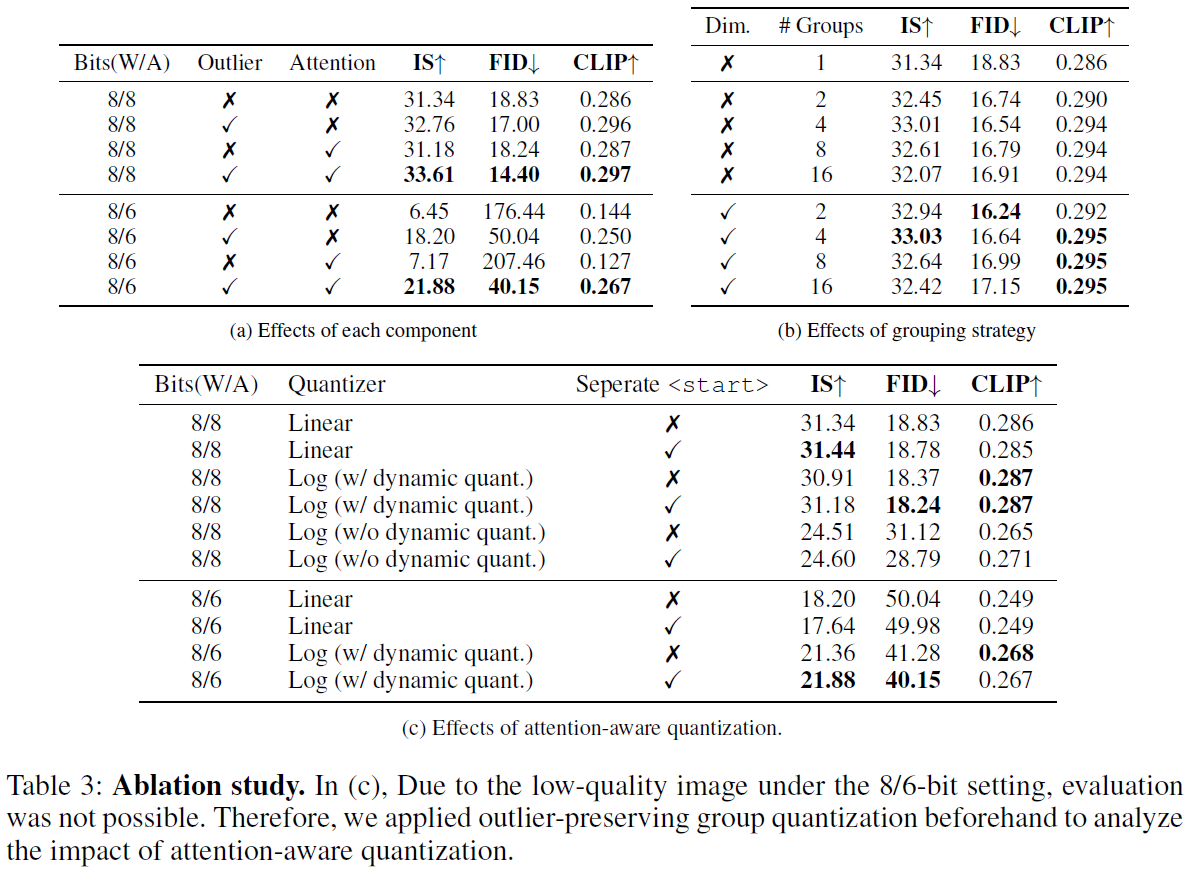
Table 3의 (c)에서는 Linear(Uniform) Quantization에 비해 Log Quantization 방식이 효과적이며, Start 토큰을 구분하여 처리하는 것이 제일 좋은 성능을 보임. (a)와 (b)는 각각 quantization bit-width와 group-size에 대한 실험결과임
Conclusion
본 논문에서는 이미지 품질에서 out-lier에 대한 역할을 파악하고 activation 분포를 보존하기 위한 방식을 제안함. 또한, Cross-Attention에서 발생하는 패턴을 발견하며, prompt에 특화된 logarithmic 기반의 quantization기법 DGQ를 제안함. DGQ는 기존 방식들과 달리 추가적인 fine-tuning 없이 text-to-image diffsion모델의 저비트 양자화를 가능하게 함.
Review
Strong Points
1) Cross-Attention에서 Start Token의 영향을 처음으로 분석
Diffusion모델에서 쓰이는 Cross-Attention 구조에서 start token이 global한 context와 background에 중요한 영향을 미친다는 점과 이 token이 quantization 적용 시 품질저하를 유발할 수 있다는 점을 처음으로 알 수 있었음.
2) Logarithmic Quantization
Outlier 민감도를 줄이고, value들의 distribution에 맞춘 효율적인 scaling을 위해 logarithmic quantization을 사용하는 방식을 처음으로 제안함.
Weak Points
1) Pixel-wise Outlier 대응
논문의 분석파트에서는 channel 단위 outlier와 마찬가지로 pixel 단위 outlier가 특정 layer에서 강하게 나타날 수 있다고 밝혔지만, 제안한 DGQ는 channel 기반의 group-wise quantization에만 초점을 맞추고 있음. 결과적으로 pixel-wise outlier에 대해서는 추가적인 대응방안이 없음.
2) Start token의 FP 유지로 인한 비교 공정성
DGQ는 Start token이 이미지 품질에서 중요한 역할을 하고 있음을 밝혔음. 하지만, 실험부분에서는 성능 비교 시 start token을 FP로 유지하였음. 이는 엄밀히 말하면 mixed precision 설정이며, 기존 baseling 방식들에 비해 quantization을 동일하게 진행한 것이 아님. 기존 baseline방식들은 start token까지 quantized된 조건에서 평가된 것으로 보이는데 직접적인 성능 비교의 공정성에 의문이 있음.



