https://arxiv.org/abs/2505.22167 ICML 2025 Accepted Paper
Q-VDiT: Towards Accurate Quantization and Distillation of Video-Generation Diffusion Transformers
Diffusion transformers (DiT) have demonstrated exceptional performance in video generation. However, their large number of parameters and high computational complexity limit their deployment on edge devices. Quantization can reduce storage requirements and
arxiv.org
Abstract
Diffusion Transformer (DiT)는 비디오 생성에서 탁월한 성능을 입증했지만 높은 계산 복잡도로 edge device에서의 구현에 제약이 존재함. 이를 위해 quantization이라는 기법으로 모델 parameter의 bitwidth를 줄여 메모리 요구사항을 줄이고 infernece 속도를 높일 수 있음. 하지만, 기존의 이미지 생성 모델의 quantization 방식은 비디오 생성 task까지 일반화되어 있지 않음.
본 논문에서는 이러한 한계를 해결하기 위해 Video DiT모델에 특화된 Q-VDiT를 제안함.
이 논문에서는 2가지 관점에서 method를 제안하는데,첫번째로 Quantization 관점에서는 Token-aware Quantization Estimator(TQE)를 제안함. 두번째로는 최적화 관점에서 프레임 간의 시공간적 상관관계를 보존하기 위해 Temporal maintenance Distillation (TMD)를 제안함.Q-VDiT은 W3A6 (3비트 weight, 6비트 activation)환경에서 SOTA를 달성함.
Introduction
이미지 생성 분야에서 성공적인 성능을 보이는 Diffusion Model(DM)과 더불어 Diffusion Transformer(DiT)는 비디오 생성분야에서 주요한 모델로 주목받고 있음. 하지만, 매우 큰 parameter들로 인해 edge device에서 활용하기는 어려움.
Quantization은 모델을 압축할 수 있는 효과적인 기법이지만. 기존의 image generation과 달리 video generation은 문맥정보(context)까지 고려해야하기 때문에 기존의 image generation분야에서 알려졌던 quantization은 바로 적용하기 어려움.
이에 대한 한계를 해결하기 위해 본 논문에서는 DiT에 특화된 quantization기법인 Q-VDiT를 제안하며, Q-VDiT는 Token-aware Quantization Estimator (TQE)와 Temporal Maintenance Distillation (TMD) 기법으로 구성됨.
논문의 contributions는 다음과 같음
Contributions
1) weight 정보가 information entropy를 충분히 전달하지 못하며 이것은 quantization error로 이어짐을 이론적으로 증명함 & TQE 방식 제안하여 quantization-error를 low-rank appproximation을 가능케함.
2) MSE loss만 활용하는것은 video generation에서 inter-frame optimization에 적절하지 않음을 분석함 & TMD 제안하여 프레임간의 distributions를 고려하는 optimization을 가능케함.
3) Q-VDiT를 제안하여 video generation task에서 post-training quantization SOTA 성능을 달성함
Methods
Model Quantization
Quantization 과정은 다음과 같이 이뤄짐
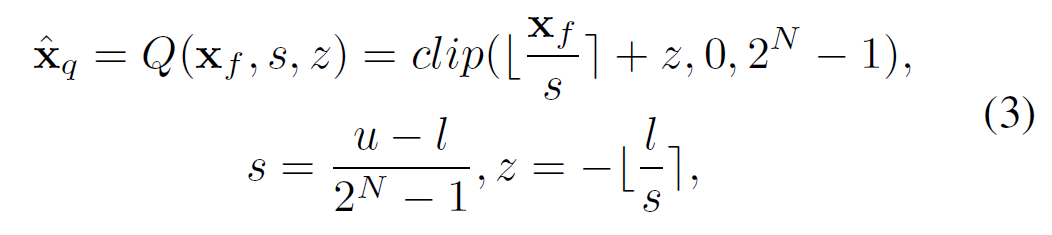
$X_f$는 원본 벡터이며, $s$는 scaling factor를 의미함. scaling factor를 원본벡터에 나눔으로써 interger값으로 치환이 가능함. $z$는 zero-point이며 원래 값의 0을 quantized 정수에서 어디에 매핑할 지 결정함. $X$는 양자화를 진행할 bit수(bit-width)를 의미함. 예를 들어 8bit 양자화를 하고 싶다면 $N$은 8이 됨.
이러한 양자화 과정을 거치면 최종적으로 $\hat{x}_q$이 산출됨.
Quantized value들을 다시 복원하기 위해서는 Dequantize과정을 거쳐야하는데 아래 수식과 같이 진행함.
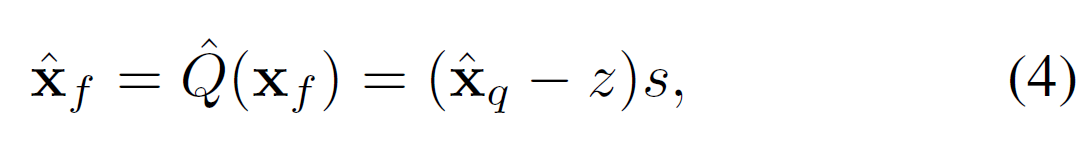
Quantization의 역순으로 진행되어 Quantized Vector $\hat{x}_q$를 full-precision(원본 실수형 표현범위)로 다시 표현함.
이미 정수화를 시켜놨기 때문에 dequantized를 해도 간결해진 값이 유지된 상태로 변환됨.
Dequantization은 단순히 inference를 위해 실수형 표현범위로 변환하는 역할
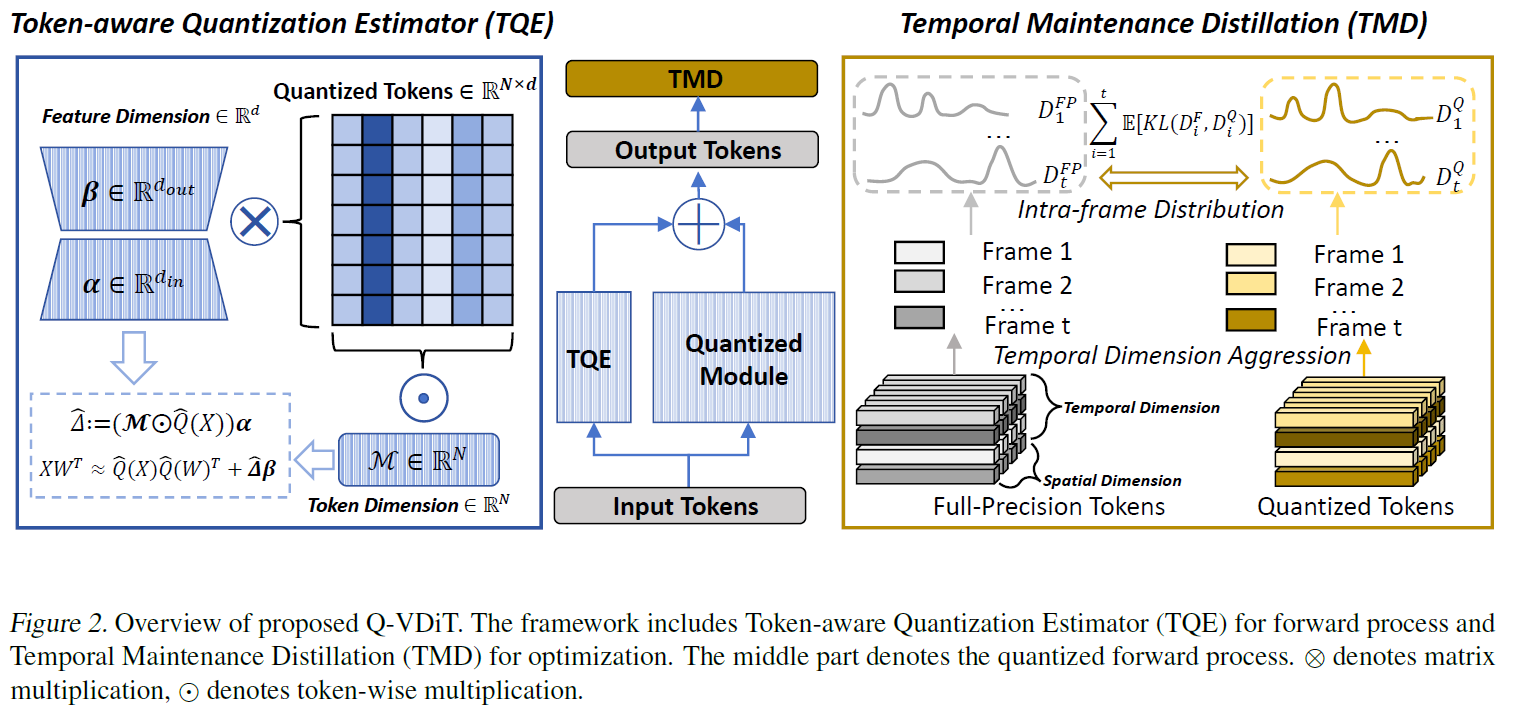
Token-aware Quantization Estimator (TQE)
Video DiT에서는 latent representation $\mathbf{Z} \in \mathbb{R}^{n \times d}$으로 표현할 수 있음. 여기서 $n$은 token의 갯수를 의미하며 $d$는 hidden dimension을 의미함.
구체적으로 $n$ 은 $s \times t$로 구성되어 있는데 여기서 $s$는 spatial token이며 $t$는 temporal token을 의미함.
따라서, video generation task에서는 $n$으로는 $t$ frame만 표현할 수 있다는 뜻이기 때문에 video에서 모든 frame을 표현하기 위해서는 token의 수가 비가역적으로 커진다는 한계가 존재함.
특히, Quantization process에서 low-bit로 표현되는 경우에는 한정적인 표현범위로 인해 엄청난 information loss가 발생할 수 있으며, 이는 Video DiT (V-DiT)에는 매우 치명적임.
본 논문에서는 모델의 information을 가능한 최소한의 parameter들로 보존하는 것을 목적으로 함.
Proposition 3.1
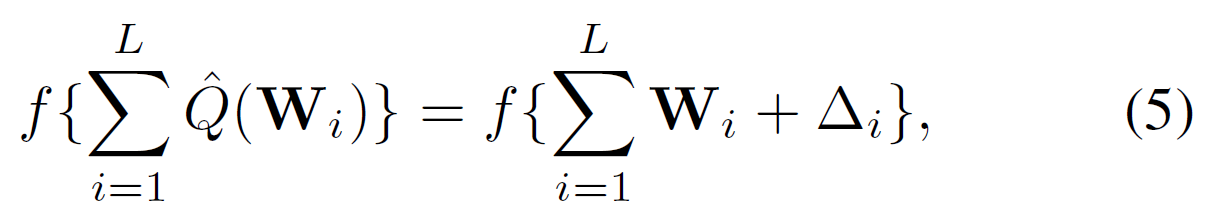
$L$ layer에 대한 weight quantization은 weight $W$에 perturbation(섭동) $\triangle$을 추가하는 것으로 볼 수 있음.
즉, layer quantziation error를 $\triangle_i$로 보면 $i$번째 layer에 대한 $W_i$는 "원래 weight + layer 별 perturbation"으로 해석할 수 있으며, 이는 low-rank approximation을 위해 사용됨.
Theorem 3.2
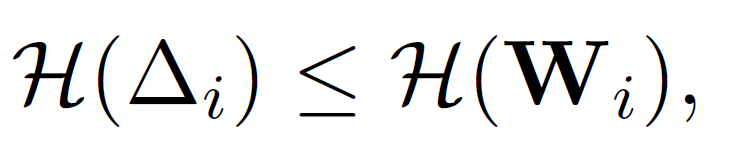
Propostion에 대한 위 정리는 다음과 같이 정리할 수 있음.
"임의의 layer의 weight $W_i$에서, 이와 대응되는 quantization error $\triangle_i$의 information entropy는 항상 작거나 같다 "
직관적으로 보았을 때 quantization은 다대일 매핑으로 이루어지고, $\triangle_i$에 대한 information entropy(무작위성)는 항상 weight $W_i$보다 작을 수 밖에 없음.
따라서, $\triangle$은 저차원 혹은 저랭크 공간에서 더 잘 표현될 수 있다는 근거가 됨.
이어서 $XW^T$는 full-precision에 대한 출력인데, quantization을 진행하는 경우 이는 $X \hat{Q} (W)^T$로 근사됨.
이는 아래 수식과 같이 근사할 수 있음.
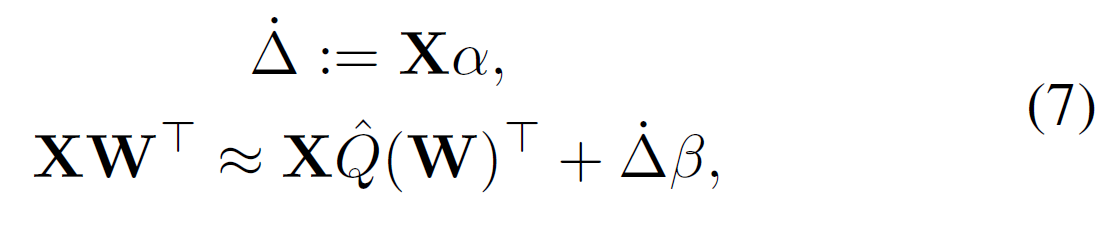
여기서 $\dot{\triangle}$는 $\mathbb{R}^{n\times1}$에 대한 token 별 오차세기를 나타내는 scalar 벡터이고, $alpha$는 입력된 feature를 token 별 scalar로 뽑는 투영벡터임. 또한, $\beta$는 그 scalar를 output 차원으로 펼치 벡터를 의미함.
결론적으로 원래는 $d_{out} \times d_{in}$ 차원의 error를 다뤄야하지만, 이를 $\alpha$와 $\beta$로 치환해 $d_{in} + d_{out}$으로 줄일 수 있게 됨. 이는 parameter에 대한 overhead를 최소화하는 방식임.
이 구조는 LoRA와 유사하지만, error에 대한 복구가 목적이고 $\alpha$는 벡터형태이기 때문에 rank-1의 얕은 구조를 띄게 됨.
하지만 이는 feature 단위의 low-rank approximation이기 때문에 이어서 frame에 대응하긴 위해 아래 수식을 활용함.
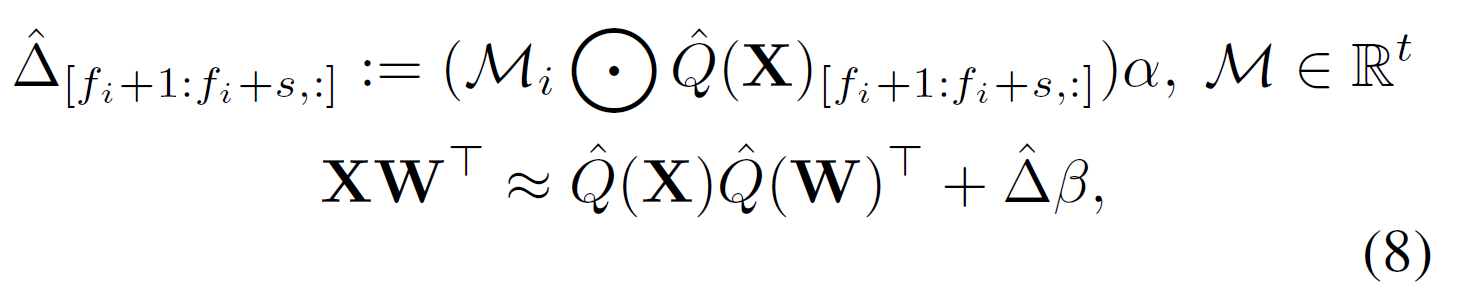
feature 축만 보는 수식7과 달리 수식8은 token축의 정보 (시간 및 공간)를 반영함. 여기서 $\mathcal{M}$은 frame별 scalar gate를 의미하며, frame별로 $\mathcal{M}_i$로 quantized activation인 $\hat{Q}(X)$를 스케일링한 후 $\alpha$를 곱함.
그 후, output 방향벡터인 $\beta$로 외적하여 최종적인 보정을 진행함.
이러한 방식을 통해 weight에서 token의 salient 값과 activation quatization 시 생기는 dissimilarity에 대해 고려할 수 있게 함.
다음은 게이트를 initialize하는 수식임.
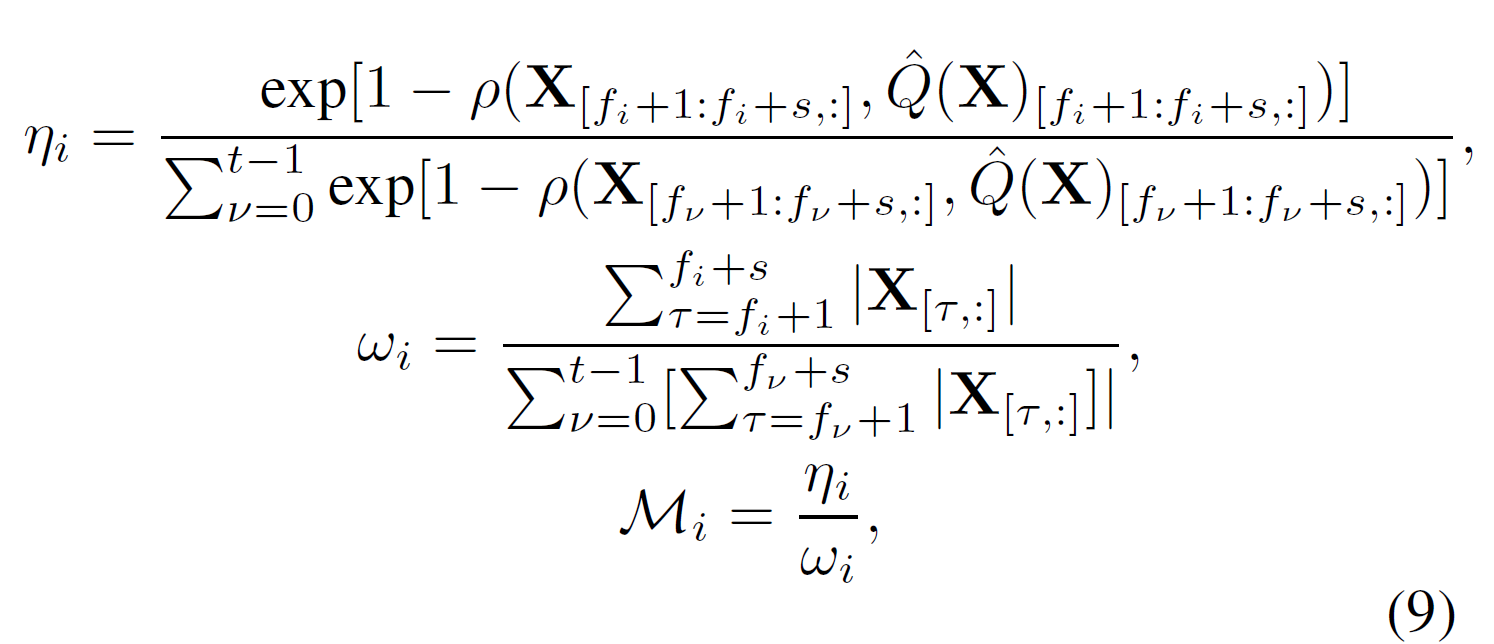
수식 9의 핵심은 오차가 큰 frame은 키우고, 원래 값이 큰 frame은 뭉개지도록 하여 frame별 게이트 $\mathcal{M}_i$를 만드는 것임.
여기서 $\eta_i$는 불일치점수이며, $\omega_i$는 saliency(frame의 규모)를 의미함.
따라서 $\mathcal{M}_i$는 오차가 크면 키우고 ( $\eta_i$ 크게), 값 자체가 크면 값을 뭉개는 ( $\omega_i$ 크게) 역할을 함.
결론적으로 $\mathcal{M}$는 "어디에 보정을 더 줄지"를 정하는 역할을 함
Temporal Maintenance Distillation (TMD)
기존의 DiT optimization 방식에서는 full-precision(FP)모델과 quantized(Q) 모델 간 output error를 최소화하는데 중점을 두며 수식10과 같이 Loss를 구함.
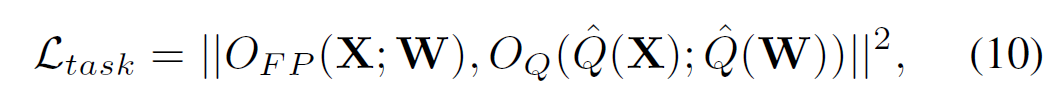
여기서 $O_{FP} \in \mathbb{R}^{n \times d}$는 FP모델의 output이며, $O_{Q} \in \mathbb{R}^{n \times d}$ 는 quantized model의 output을 의미함. 수식 상의 편의를 위해 이를 $S^{FP}$와 $S^{Q}$로 표기하며, frame 단위로 표현하면 수식11과 같음.
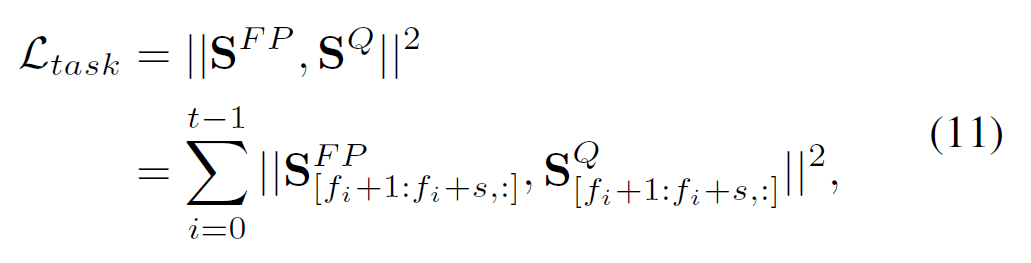
여기서 $s$는 frame당 token을 의미하며, 총 frame은 $t$로 표기함.
이때 Q모델의 frame $i$ gradient는 다음과 같이 표기함.
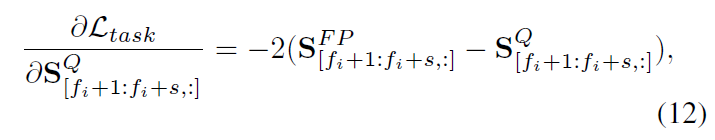
여기서 문제는 수식 11, 12는 각 frame을 독립적으로 처리하기 때문에 temporal 정보를 반영하지 못함. 특히, 비디오의 경우 frame들간의 상관관계가 매우 강하기 때문에 이러한 방식으로는 global한 시간일관성이 깨질 수 있음.
특히, 이러한 기존의 방식은 비디오 생성에서 inter-frame information이 서로 연관되어있는(dependent)한 관계를 무시하며, 좋지 않은 optimization결과를 도출함.
따라서, 본 논문에서는 Temporal Maintenance Distillation(TMD)라는 방식을 제안하여 inter-frame information을 고려할 수 있도록 함.
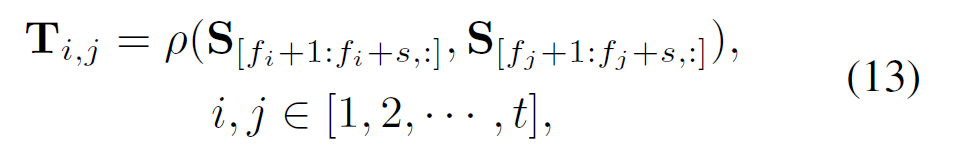
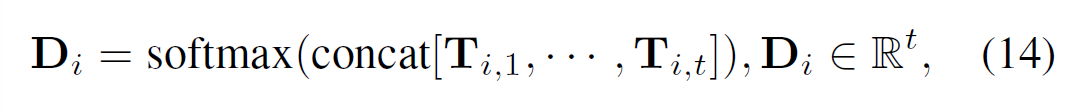
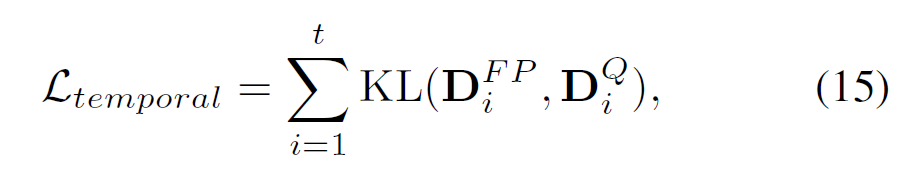
수식 13과 14에서는 frame $i$와 $j$의 유사도를 frame $i$의 입장에서 softmax로 취함.
softmax를 취한 값들은 수식 15와 같이 KL 발산을 통해 두 분포를 맞추는 과정을 거침. 이를 통해 frame $i$ 최적화 시 다른 모든 frame간 관계까지 동시에 고려할 수 있으며, global한 시간구조를 보존하는 방향으로 학습을 유도함.
Gradient가 전역적(연쇄적)으로 퍼지는 방식은 아래 수식16 및 17과 같음.
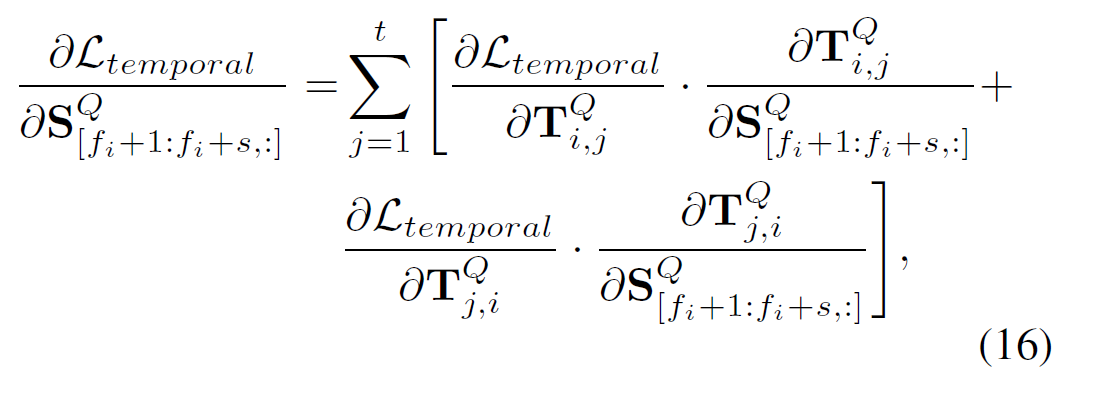
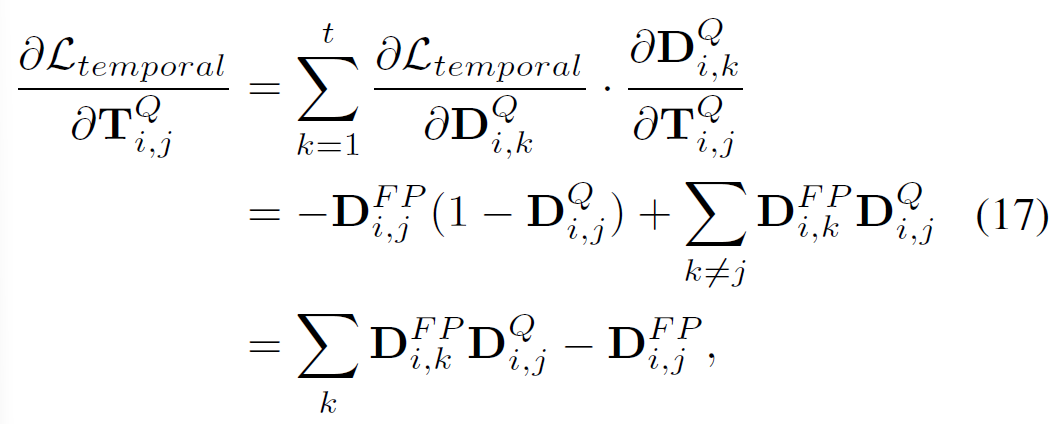
최종적으로 optimization은 비디오 전역의 시간구조를 고려하며 다음과 같이 진행됨.
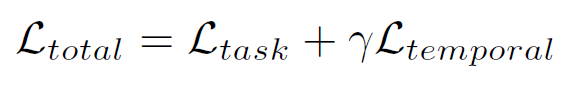
$\gamma$는 hyper-parameter이며 실제로 사용 시 100의 값을 사용할 것을 권장함.
Experiments
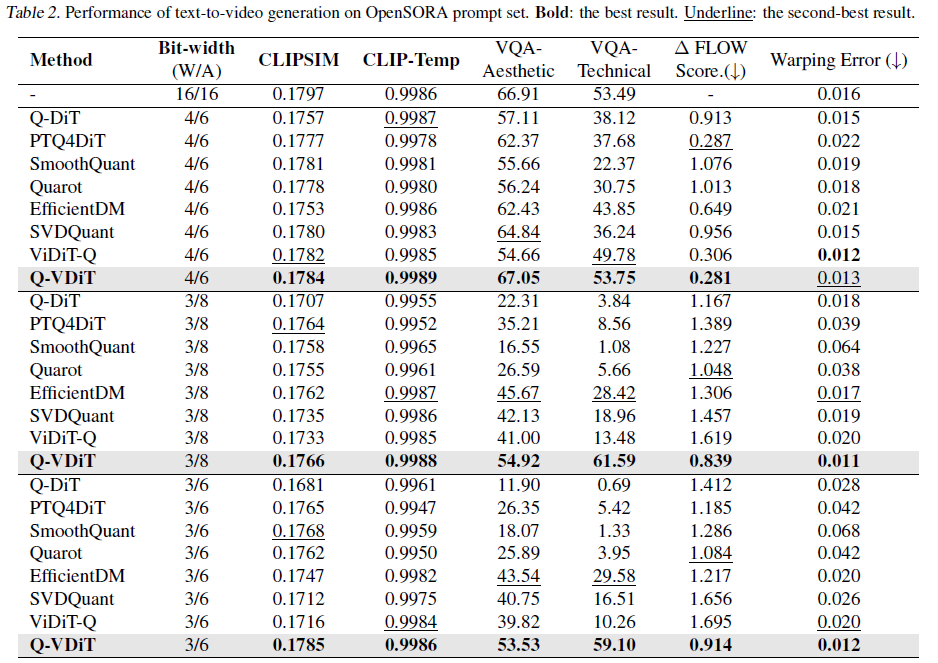
실험결과, Q-VDiT는 3비트 weight 6비트 activation에서 SOTA성능을 달성하였으며, 가장 극단적인 압축환경에서 인상적인 성능을 보임.
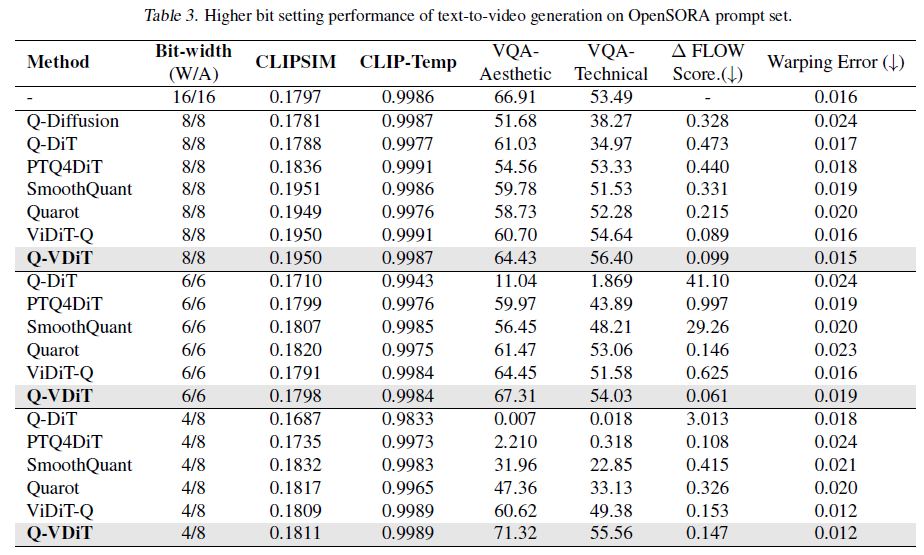
비교적 높은 비트환경에서도 우수한 성능을 보임을 확인함.
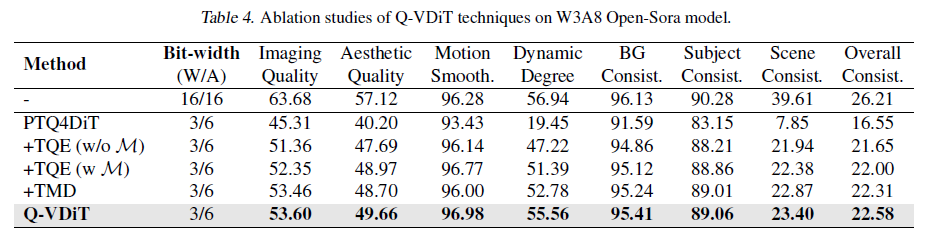
VBench 기반의 Ablation study에서도 TQE와 TME를 모두 활용하였을 때 가장 우수한 성능이 보임을 분석함.
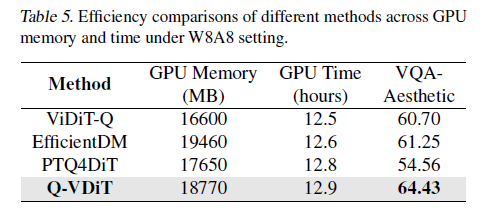
메모리 사용 측면에서도 Q-VDiT은 최소한의 paramter 추가로 gpu time과 memory 소비를 최대한 막으면서도 우수한 성능을 도출함.
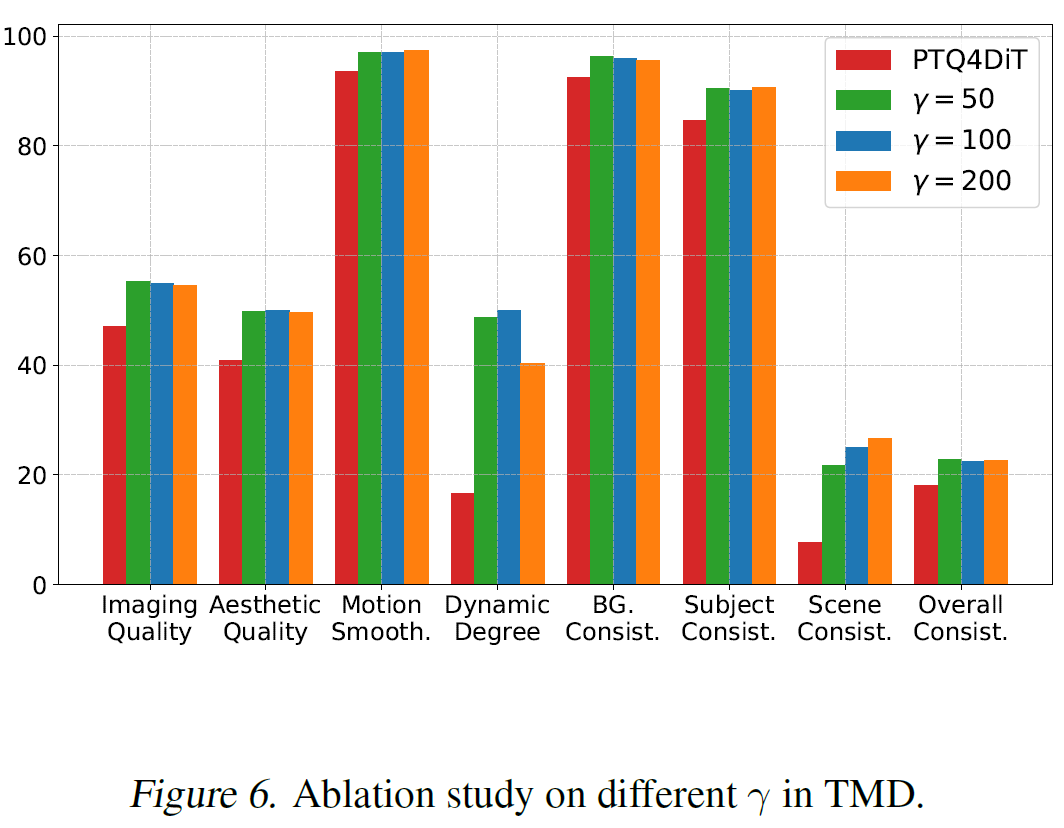
Figure 6의 경우 $\gamma$가 TMD에서 민감한 것을 확인하였으며, 100의 값을 쓰는 것이 가장 균형있는 선택이라고 논문의 저자들은 주장함.
Conclusion
본 논문에서는 DiT에 특화된 quantization 방식인 Q-VDiT를 제안함.
Q-VDiT는 quantization 시 information loss 문제를 해결하기 위해 Token dimension과 feature dimension을 모두 고려하는 Token-aware Quantization Estimator(TQE)를 제안함. 또한, 비디오 내 다른 frame에 대한 spatiotemporal(시공간적) correlation을 최적화하는 Temporal Maintenance Distillation (TDM)을 제안함.
Review
Strong Points
1) TQE는 rank-1 LoRA와 사실상 비슷한 구조이기 때문에 메모리 overhead를 매우 효과적으로 줄일 수 있음. 따라서, 보정을 위한 parameter 추가에도 메모리 사용량의 절감과 추론속도의 향상까지 가능해 optimization에 매우 유용한 구조를 DiT모델에 적용한 것 같음.
2) TME에서 KL분포를 활용하여 한 frame에서 다른 모든 frame과 연쇄적으로 상호작용하도록 한 것이 새로운 접근임. 이를 통해 비디오 생성에서 중요한 공간&시간적 정보를 모두 반영할 수 있다는 점이 매우 큰 기여라고 생각함.
Weak Points
1) TME에서 temporal한 정보가 video generation에서 유의미한 correlation을 갖는다는 것을 실험적으로 검증한다면 논문의 주장을 강화할 수 있을 것 같음. (ex. frame 변화에 따른 quantization error graph) 현재 논문에서는 correlation 자체를 정량적으로 검증하는 실험결과는 없는 것이 아쉬움.
2) TQE는 수식적으로나 이론적으로는 매우 잘 정리되었지만, 실제 배포상에서 어떤 방식으로 동작하는지에 대한 설명은 비교적 부족함. pseudo code나 algorithm을 통한 동작구조까지 있었다면 훨씬 이해하기 편했을 것 같음.



