Newton Method(뉴턴법)

Newton Method: 함수의 해를 근사하는 방법

 

Newton Method의 활용

 

1. 이미지 변환(ex. 카메라 왜곡보정)

이미지를 미분하여 새로운 이미지로 변환시킬 때

 

2. 목적함수 최적화

 

 

Newton Method의 한계

 

1. 함수의 해가 여러개일때 한개의 해만 구할수 있음.

2. 초깃값 설정에 따라 해를 구하기까지의 시간이 달라짐.

3.해를 구하려는 함수가 미분이 가능해야 함.

 

 

Newton Method 개념

 

 

이 함수의 해를 구하기 위해 x = 4 에서의 접선을 구한다.

 

이와 같이 그려진다.

 

x= 3.xx 일때의 접선을 전과 같은 방법으로 다시 접선을 그린다.(파란색 선)

 

이와 같은 방법을 반복하면 다음과 같이 3이라는 해에 점점 가까워지는 것을 볼수있다.

 

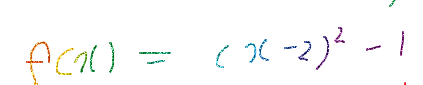
위 그래프와 같은 경우에는 직관적으로 해를 찾는 것이 가능하지만 함수가 복잡해질 경우 해를 찾기 매우 어려운데

이 경우 Newton Method를 활용하여 해의 근사값을 구할 수 있다.

 

다음과 같은 함수는 해를 구하기 힘들기 때문에 Newthon Method를 활용한다.

 

 

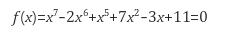
위 그래프와 같이 접선을 이용해 해를 구하는 과정은 Taylor Expansion(테일러 전개)를 활용한다.

 

1차식일때의 테일러 전개식(특정 x값이 a일 때)

 

2차식일때의 테일러 전개식

 

n차식일때의 테일러 전개식

 

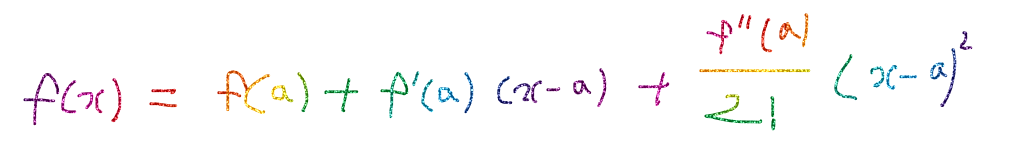
주어진 그래프는 2차식이기 때문에 우리는 1차식일때의 테일러 전개식을 활용한다.

 

위와 같이 첫번째 접선의 식을 도출한다.

 

Newton Method는 이와 같이 테일러전개식을 활용해 특정위치 a 에서부터 해를 찾을때까지 1차함수로 근사한다.

 

이 때,  해를 찾기 위해서는 다음과 같이 테일러 전개식을 이용한 1차함수가 0이 될때이다.

 

그러므로 1차식에서의 테일러전개식이 0이 되도록 하여 다음과 같이 다시 쓸 수 있다.

여기에서 x는 다음에 들어올 값, a는 현재값으로 정하면 식은 다음과 같이 바뀐다.

 

 

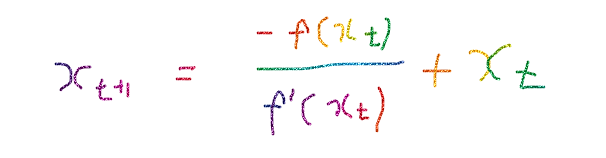
이 식을 위 예시에 적용 시켜보면

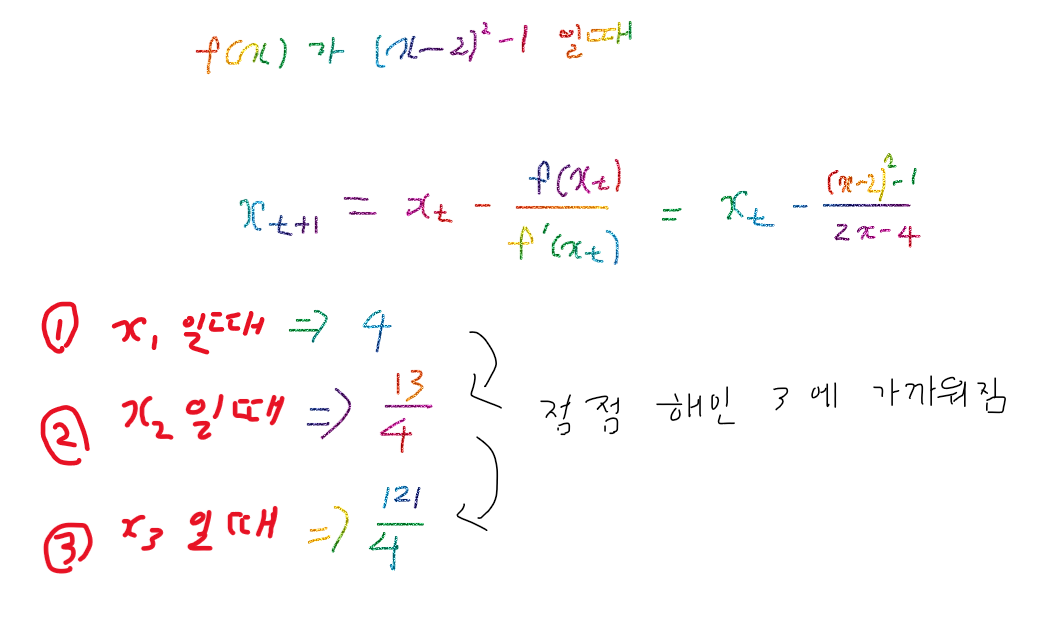
이런과정을 거쳐 점점 3이라는 해에 가까워 지는 것을 확인 할 수 있다.

 

 

 

이 글은 유튜브 뉴턴 방법(Newton Method) | 인공지능 및 컴퓨터 비전을 위한 수학 핵심 개념 노트(Mathematics for AI)

와 블로그 darkpgmr.tistory.com/58  를 참고로 하여 작성하였습니다.