GCN은 왜 생기게 되었을까?
인공지능 분야에서 이미지데이터를 처리할 때에는 CNN (Convolutional Neural Network)을 가장 대표적으로 사용합니다.
그리고 순차적인 데이터 (ex. 음성 데이터, 텍스트 데이터)같은 경우에는 RNN (Recurrent Neural Network)을 대표적인 모델로 떠올릴 수 있습니다.
하지만 위와 같은 데이터들이 아닌 연관관계가 있는 데이터들이 있다면 CNN, RNN같은 기존 모델들이 좋은 성능을 보일까요? 모델의 개념에 대해 공부해보신 분들은 연관관계를 고려하지 못할 것이라는 것을 쉽게 유추하실 수 있을 것입니다.
연관관계가 있는 데이터의 예를 든다면
1. SNS의 Social Network
2. 인간의 뇌세포 구조
3. 3차원형태의 픽셀 그림(3D Mesh)
등이 있습니다.

이러한 연관관계가 있는 데이터들을 다루기위한 모델이 바로 GCN (Graph Convolution Network)입니다.
GCN은 다른 모델들에 비해 연관관계를 확실히 잘 반영한다는 평가가 많은데요.
수치상으로 봤을 때에도 실제로 연관관계가 있는 데이터들을 가지고 실험한 결과 GCN이 월등히 높은 성능을 보였습니다.
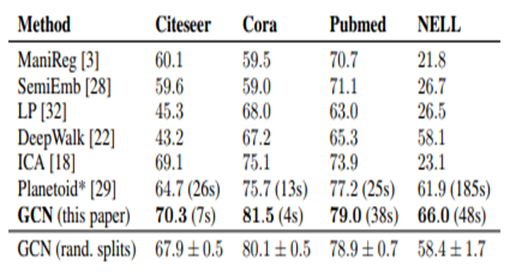
이제 GCN이 연관관계 데이터를 효과적으로 다루는 모델이라는 것을 알았으니, 모델의 개념과 구조에 대해 살펴보도록 하겠습니다.
GCN의 개념
그래프 데이터를 컴퓨터에 반영하는 법
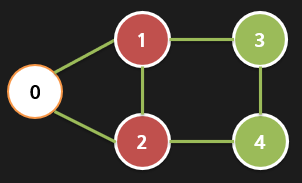
GCN의 개념에 대해 알아보기 전에 먼저 그래프데이터를 어떻게 처리 할지 알아볼텐데요,
먼저 위와 같이 5개의 노드(vertex)로 이루어진 그래프가 있다고 가정을 하겠습니다.
여기서 연관관계를 반영하기 위해선 어떤식으로 정보를 컴퓨터에 담아야 할까요?
컴퓨터가 가장 빠르고 편리하게 정보를 담을 수 있는 방법은 바로 행렬을 이용하는 것입니다.
그래서 GCN은 다음 그림과 같이 두개의 행렬을 이용하여 위 그래프의 정보를 담을 수가 있습니다.
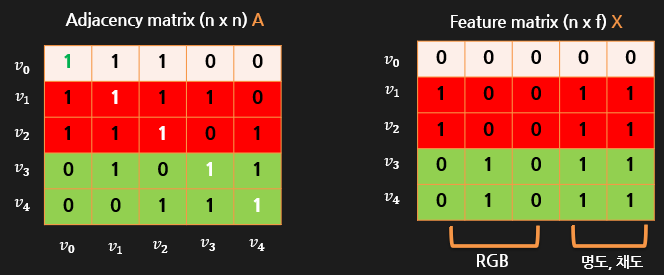
이 두개의 행렬을 사용해서 정말 간단하게 그래프의 모든 정보를 담았습니다.
왼쪽의 Adjacency matrix(인접행렬)은 그래프의 연결관계를 표현한 행렬입니다 v0노드부터 각 노드를 기준으로 어떤 노드들과 연결되었는지 간결하게 행렬에 저장한 것을 볼 수 있는데요. 처음에 개념이해를 위해선 그래프를 보고 연결관계에 따라 직접 인접행렬을 그려보시는 것을 추천드립니다. 약자로는 A를 사용하는데요 이따 밑에서 모델구조 설명할때 나오니 잘 기억하시길 바랍니다.
오른쪽의 Feature matrix는 말그대로 노드들의 특성정보를 반영하는 행렬입니다.
여기서는 5개의 특성(열)을 두어 RGB 정보들과 명도, 채도를 반영하였습니다.
RGB 값이나 명도, 채도는 0~255 사이의 값으로 보통 표현하지만 전 편의상 0과 1로만 표현을 했습니다.
이 부분은 코딩할 때 입맛에 맞춰서 사용하시면 될 것 같아요
아무튼, 이런 식으로 하나의 행렬을 사용해 노드의 색깔과 정보들을 편리하게 담을 수 있었습니다.
약자로는 X나 H를 사용하는데 주로 H로 사용한다고 기억하고 계시면 될 것 같습니다.
이제 이 데이터들을 토대로 학습을 어떤식으로 진행하는 지 알아보도록 하겠습니다.
GCN은 Graph Convolution Network의 약자입니다.
Convolution이라는 단어하면 CNN이 생각나지 않으신가요?
눈치 채셨겠지만 GCN도 CNN과 상당히 유사한 구조를 지닙니다.
예시를 들면 요런식으로 모델구조를 나타낼 수 있습니다.
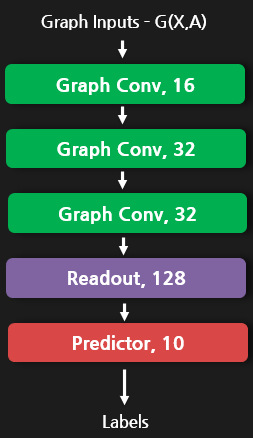
하지만 여기서 문제점이 몇가지 생깁니다.
1. 두개의 행렬을 어떻게 합쳐서 Convolution할 것인가
2. 그래프 데이터는 노드(vertex)의 위치가 바뀌면 행렬값이 여러개로 바뀔수도 있는데 어떻게 일반화를 시킬 것인가
GCN의 핵심으로는 이런 문제점들을 해결하면서 CNN과 같은 구조를 갖춰 Convolution을 시키는 것인데요
요 부분들만 이해를 하시면 GCN의 개념에 대해 다 이해를 하셨다고 봐도 무방합니다.
이제 차근차근 첫번째 문제점부터 해결을 하는 과정에 대해 알아보겠습니다.
1. 두개의 행렬을 어떻게 합쳐서 Convolution할 것인가
두개의 행렬을 Convolution하는 과정은 당연하겠지만 이 Graph Conv 과정에서 이루어집니다.
여기서 새로운 그래프를 예시로 들겠습니다
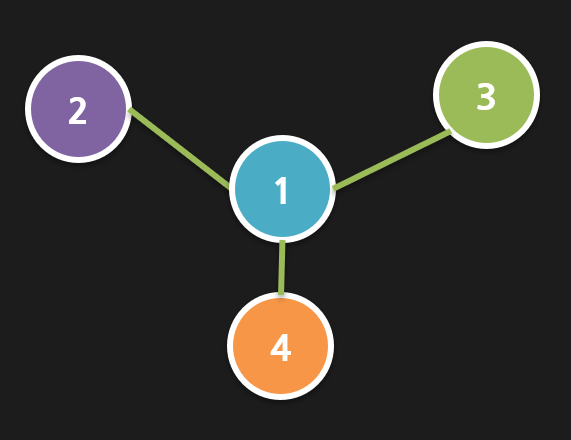
위와 같은 그래프가 있다고 가정하면 여러 층의 Conv 과정을 거치기 위해서는 어떤 식으로 구현을 해야할까요?
모델은 CNN과 상당히 유사한 구조지만 이 데이터는 연관관계(Edge)가 있다는 것을 기억하셔야합니다.
따라서 노드(vertex)의 자체정보와 연관관계를 동시에 적용하기엔 상당한 어려움이 있습니다.
먼저 노드의 자체정보만 저장해서 현재 Layer에서 다음 Layer로 보내기 위해서는 이런 식으로 식을 쓸 수 있습니다.
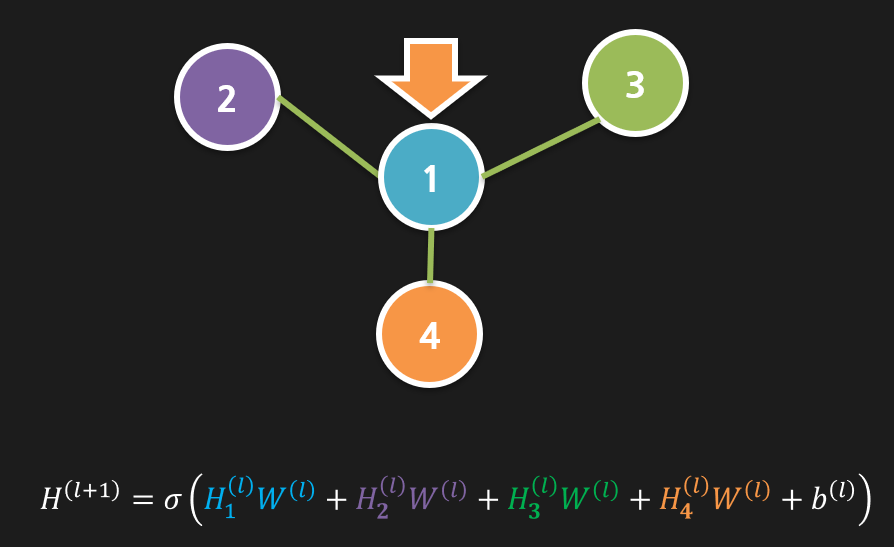
이 그림은 Vertex 1 을 기준으로 했을 때의 식입니다. H는 위에서 나왔던거처럼 Feature matrix를 뜻하고 W는 가중치를 뜻합니다.
식을 보시면 Vertex 1과 연결되는 V2, V3, V4 모든 Vertex가 식에 들어가 있는것이 확인가능합니다.
(자기자신도 당연히 다음 Layer에 보내기 위해서는 정보를 포함해야하기 때문에 식에 포함됩니다.)
여기서 모든 Vertex에 똑같은 W값이 붙는 이유는 4개의 모든 정보가 Vertex라는 같은 형식이기 때문입니다.
그럼 Vertex 2 의 경우도 한번 보겠습니다.
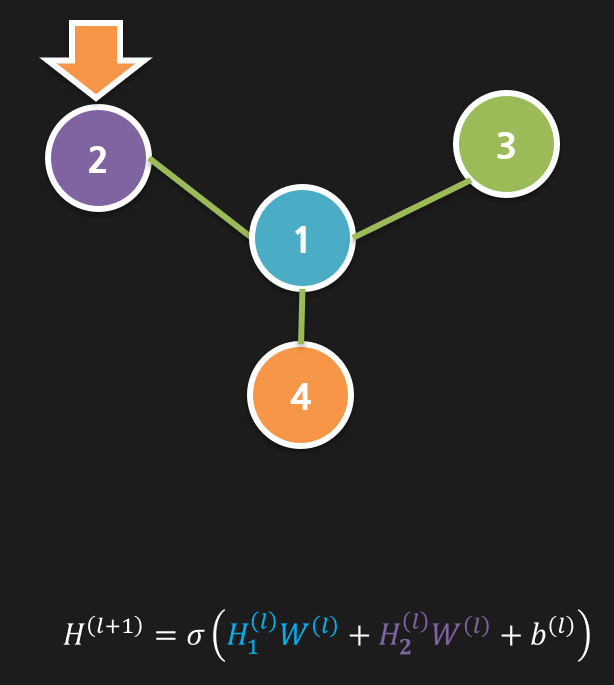
Vertex2와 같은 경우에는 이런식으로 더 간단히 표현 할 수 있습니다.
하지만 이 방식은 효율적이지 못해 실제로 컴퓨터가 사용하는 방법이 아닙니다.
각각의 노드를 기준으로 일일히 식을 나타내야 하기 때문에 너무 복잡하고, 데이터가 커지면 속도도 현저하게 느려지기 때문입니다.
이를 해결하기 위해 컴퓨터는 모든 노드(Vertex)들이 서로 연결되어 있다고 먼저 가정합니다.
위 그래프는 노드가 4개가 있기 때문에 식은 다음과 같이 나올수 있습니다.
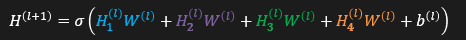
이제 이렇게 하나의 식으로 모든 노드의 정보를 포함하는 식을 만들었습니다.
이제 위의 저 식을 보기좋게 각각의 블럭으로 쪼개서 나타내 보겠습니다.
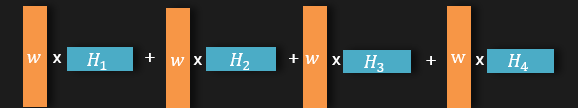
이렇게 블럭으로 보니 훨씬 이해하기 편해졌습니다. 여기서 만족하지 않고 더 보기 편해지게 같은 색의 블럭끼리 묶어보면 이렇게 큰 두 블록이 나옵니다.

최종적으로는 밑 그림처럼 같은 색끼리 곱해지는 행렬곱의 형태가 나타납니다

이제 저 긴 블록들을 큰 블럭으로 합쳐서 조금 더 자세하게 표현해보겠습니다.
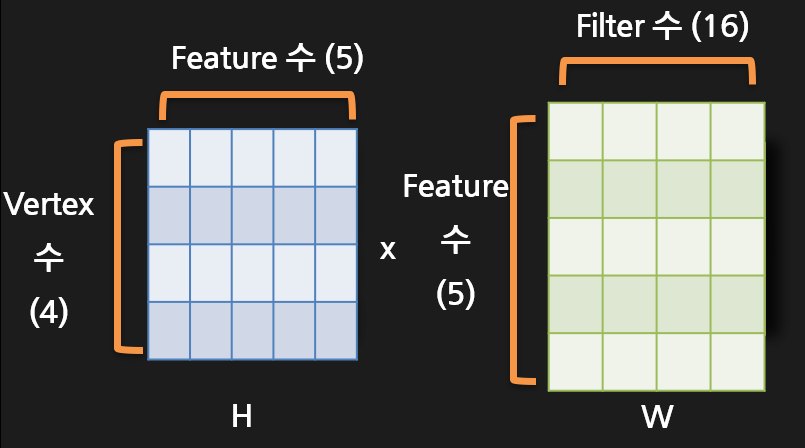
이렇게 큰 두개의 블럭이 만들어졌는데요, 이제 두 블럭의 열과 행이 어떻게 이루어졌는지 한 번 알아보겠습니다.
먼저, H블럭은 Vertex1 ~ Vertex 4 까지 노드가 총 4개 구성되어 있기 때문에 행도 당연하게 4개의 행으로 이루어져 있습니다.
열은 지금 총 5개로 이루어져있는데, 열이 5개인 이유는 Feature 값을 제가 임의로 5개를 지정했기 때문입니다.
( R, G, B, 명도, 채도 )
만약 RGB 정보나 색 정보가 아닌 다른 정보가 있다면 그 정보 수 만큼 열이 이루어지겠죠?
그리고, 가중치행렬인 W블럭은 H행렬의 Feauture 수인 5를 가져와 5개의 행으로 이루어집니다.
이유는 행렬곱을 편리하게 하기 위해서는 이전 행렬의 열 (=5) 과 다음행렬의 행의 수 (=5) 가 맞아야 하기 때문입니다.
그리고, 열은 Filter의 수로 우리가 현재 있는 레이어의 Filter를 의미합니다.

현재 우리는 Graph Conv의 첫번째 레이어에 있다고 가정하겠습니다. 레이어에 적혀있는 대로 필터의 수는 16이 됩니다. 여기서 다음 레이어로 가면 Filter수는 16이 아니라 32로 바뀌겠죠?
이제 이 두 행렬을 곱하면 이렇게 큰 행렬이 하나 생깁니다.
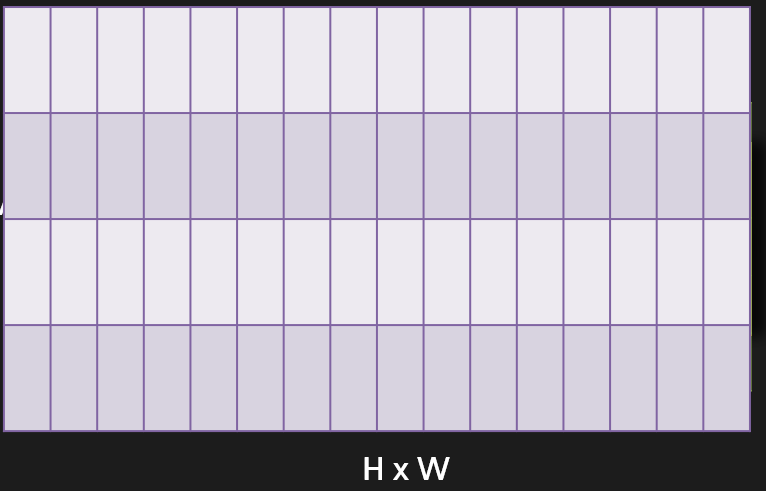
이제 우리는 노드의 정보에 가중치까지 곱한 정보를 가진 행렬을 만들었습니다.
하지만 이 행렬을 만들 때 모든 노드를 연결했다는 가정을 하고 만들었다는 것을 기억 하셔야 합니다...
그럼 여기서 원래의 그래프같은 정보를 가져오기 위해서는 어떻게 해야할까요?
답은 정말 간단합니다.
저 행렬에서 아까 만들어두었던 Adjacency Matrix (A)만 곱해주면 되는데요.
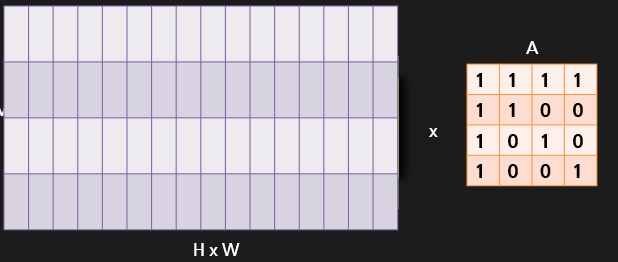
여기서, 식을 도출하기 위해서도 행렬곱 개념이 필요합니다.
행렬곱 과정을 모르시는 분들을 위해 간단하게 설명을 드리겠습니다. 행렬곱 과정을 아시는 분은 이 부분은 패스하셔도 됩니다.
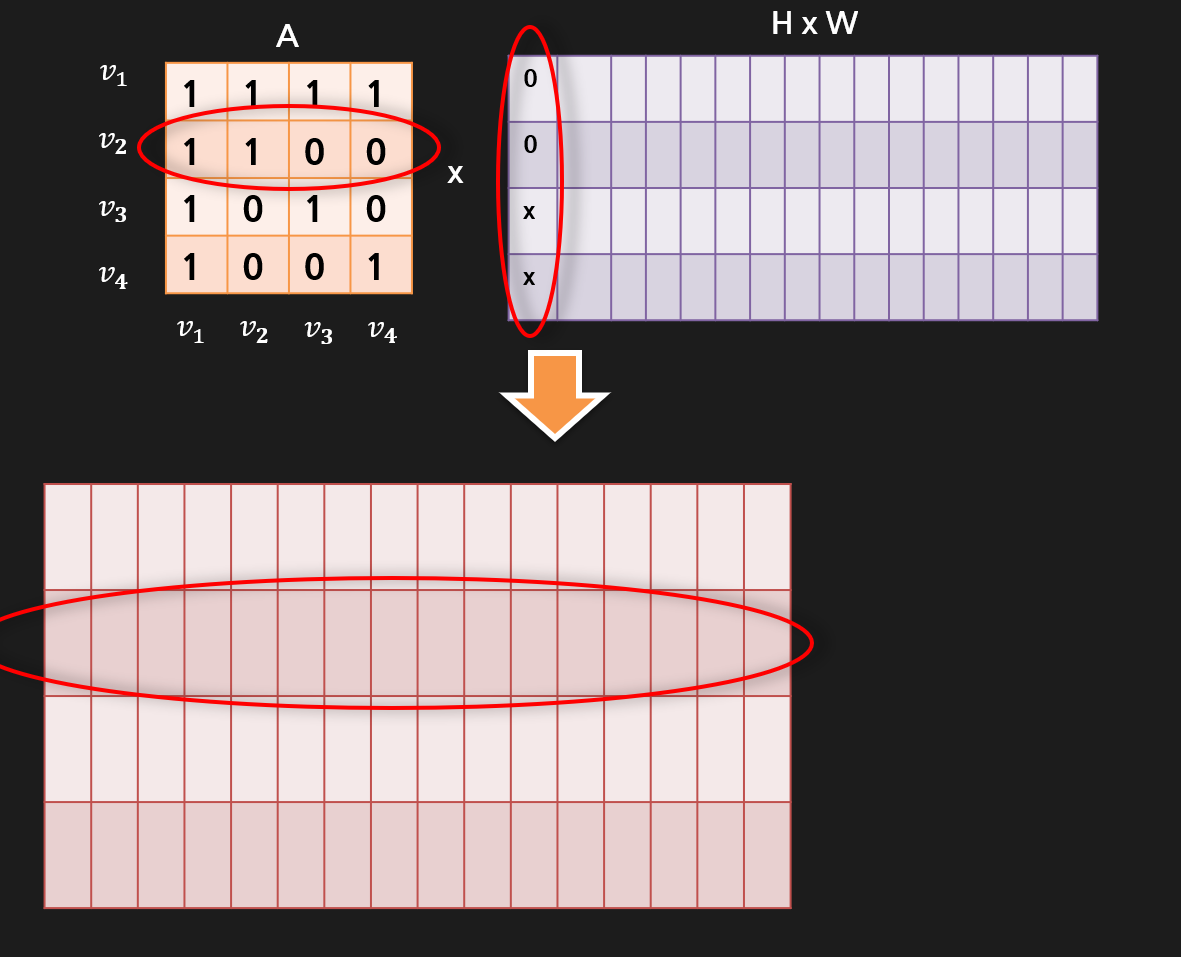
위에 있는 두 행렬은 방금까지 설명한 개념을 그대로 옮겨온 구조입니다.
여기서 V2를 기준으로 설명을 드리겠습니다.
V2를 기준으로 왼쪽 A행렬의 두번째 행과 오른쪽 테이블의 열들이 곱해지게 되는데요.
왼쪽 A행렬을 보시면 V2는 V1과 V2이 연결되어 1로 표현된것을 보실수가 있습니다.
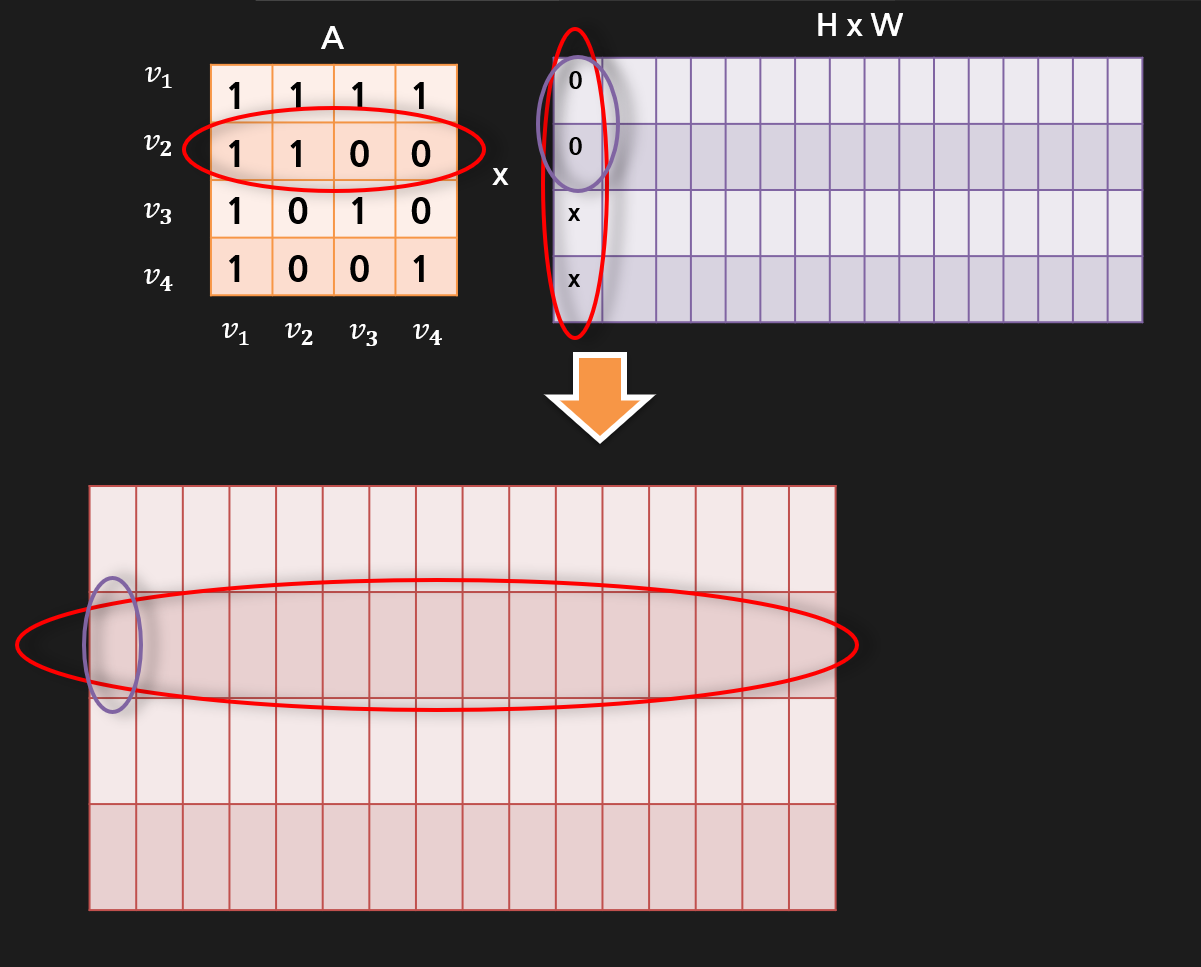
행렬곱을 할때에는 왼쪽 2번째 행을 기준으로 오른쪽 행렬의 열들이 차례대로 곱해져서 분홍색 행렬에 들어가게 됩니다.
이는 HW행렬과 A행렬이 곱해질때 위 보라색행렬의 첫번째, 두번째 행의 값만 살려서 최종 분홍색 행렬에 저장한다는 뜻입니다.
상황을 더 진행해보면,
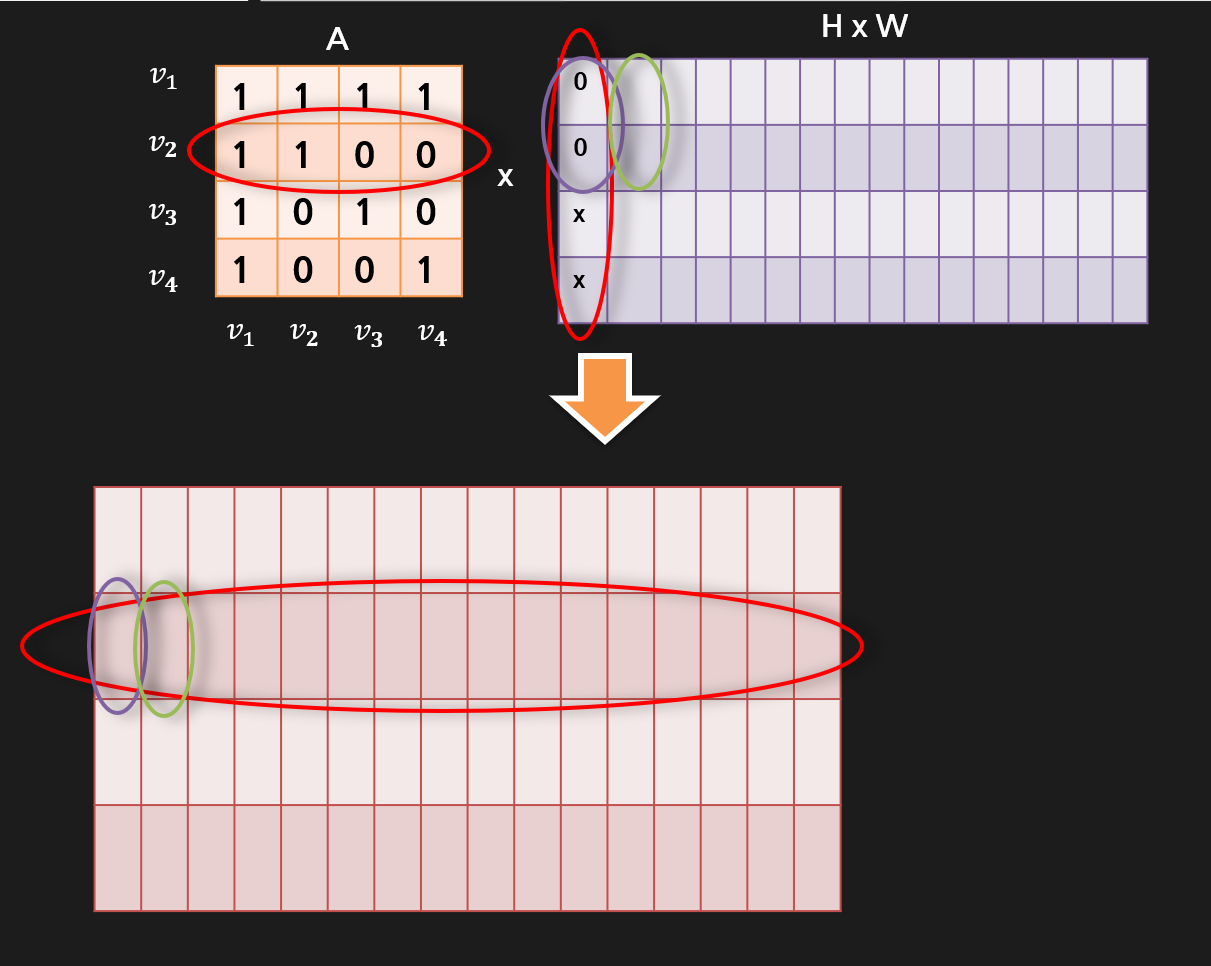
마찬가지로 초록색부분이 이런 식으로 저장되고, 쭉 다음과정도 진행되어서 분홍색 행렬이 채워지게 됩니다.
여기서 값들이 저장되는 분홍색 행렬은 다음레이어의 보낼 최종 값들로 다음레이어에 전달이 되는 행렬입니다.
이 그림들을 식으로 표현한다면 이렇게 표현할 수 있습니다.
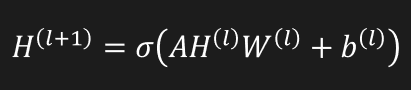
결론적으로 A행렬 x HW행렬에 b(바이어스)값과 활성화함수를 곱한값으로 정말 쉽게 식이 도출되었습니다.
이렇게 해서 과정은 복잡했지만 결과적으로는 너무 간단한 식으로 두 행렬을 Convolution에 적용시킬 수 있었습니다.
2. 그래프 데이터는 노드(vertex)의 위치가 바뀌면 행렬값이 바뀔수도 있는데 어떻게 일반화를 시킬 것인가
방금까지 도출했던 식을 통해 이제 여러번의 Conv 과정을 거쳤습니다,
하지만 Readout이라는 처음 보는 레이어를 만나게 되었습니다..
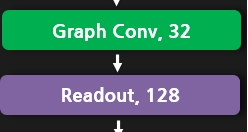
이 Readout이라는 레이어는 결론부터 말씀드리면 2번째의 문제점을 해결하는 키 레이어입니다.
즉, 여러 행렬값들을 일반화 시킬 수 있는 레이어라는 뜻입니다.
그래프 데이터는 노드간의 연결정보가 같아도 노드의 위치나 행렬의 표현순서가 달라지면 같은 그래프라도 여러가지 행렬로 표현 될 수 있습니다.
그래서 먼저 Conv 과정을 거친 후, 그래프를 일반화 시키기 위해 마지막 Conv에서 나온 행렬값을 MLP를 통과시켜 행렬의 모든 값을 합치게 됩니다.
이 과정을 Readout과정이라고 하고, 이 과정을 거친 뒤 CNN과 같이 Predict하는 과정을 거치게 됩니다.
이 Readout과정을 통해 우리는 여러가지 형태가 나오는 행렬에 대해 고민할 필요가 없어졌습니다. 정말 간단하게 2번째 문제를 해결하였습니다.
이제 모든 문제점을 해결했고, Graph데이터를 가지고도 CNN과 같이 깊이 있는 모델을 구성할 수 있게 되었습니다.
지금까지, 연관관계 데이터를 Convolution 시 생기는 문제점을 해결하는 방식으로 GCN의 개념을 알아보았는데요,
다음 글에서는 Hyper Network에 대해 알아보도록 하겠습니다.
참고논문:
Thomas N. Kiopf, Max Welling,
“Semi-Supervised Classification with Graph Convolutional Networks”
Published as a conference paper at ICLR 2017
참고 영상:
[#30.Lec] Basic of Graph Convolution Network - 딥러닝 홀로서기
강의 자료 링크 : https://github.com/heartcored98/Standalone-DeepLearning/blob/master/Lec9/Lec9-A.pdf 자료 저장소 링크 : https://github.com/heartcored98/Standalone-DeepLearning 피드백 링크 : https://goo.gl/forms/09g6VmE4tdIQAi8E3 강의
youtu.be
참고 글:
https://ganghee-lee.tistory.com/27
GNN, GCN 개념정리
GNN이란? GCN이란? GCN의 다양한 모델들 (Advanced Techniques of GCN) GNN이란? Graph neural network란? Image, Sequential data(=Sentence) 이외에 input data구조가 graph인 경우, 이 graph data를 학습해야할..
ganghee-lee.tistory.com
'AI' 카테고리의 다른 글
| Medical Image Registration (2) | 2024.03.12 |
|---|---|
| Anaconda 및 Tensorflow 설치 (0) | 2021.02.10 |
| Newton Method(뉴턴법) (1) | 2021.02.08 |
| 인공지능의 개념 (0) | 2020.12.31 |



