[IEEE Transactions on Medical Imaging 2019] VoxelMorph: A Learning Framework for Deformable Medical Image Registration

2024.03.12 - [AI] - Medical Image Registration

Medical Image Registration

 

 

https://ieeexplore.ieee.org/abstract/document/8633930 IEEE Transactions on Medical Imaging 2019

VoxelMorph: A Learning Framework for Deformable Medical Image Registration

 

Contributions of VoxelMorph

1) 이미지 정합을 위해 Global Optimization을 통한 Unsupervised Learning
     ▶ 기존 SOTA(State-Of-The_Art)모델과 비슷한 성능으로 훨씬 빠르게 registration이 가능함을 제안
2) Auxiliary Segmentation (보조 분할)을 통해 registration 성능을 향상시킬 수 있음을 제안

 

Background & Introduction

의료영상분야에서의 registration은 비선형적인 관계가 존재함
∴ 전통적인 기존 registration 방식은 energy function을 통해 진행하지만, 최적화 관련 한계가 있음
   (e.g., computational resource, training time)

Energy function: 두 영상 간 유사성을 수치적으로 평가하여 registration하며, 유사도측정(Similarity Measure)와 정규화 항(Regularization Term)으로 구성됨

 

Equation of energy function

 

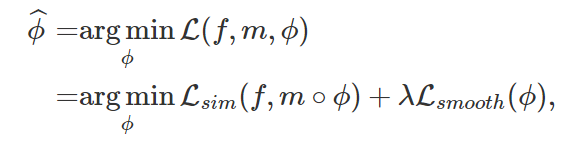
위 수식은 energy function 기반의 registration 수식이며, 표기는 다음과 같음

f = registration의 기준이 되는 'fixed'
m = registration을 진행할 'moving'
ϕ = registration field ( f 좌표를 m의 좌표로 매핑 )
m∘ϕ = 'moving'이 ϕ만큼 조정
Lsim(⋅,⋅) = 2개의 input에 대한 영상 유사도 함수 (e.g., MSE, mutual information, cross-correlation)
Lsmooth(⋅)  = 정규화함수 (regularization function) (e.g., sparially smooth deformation)
λ = 정규화 강도를 위한 hyper-parameter

이러한 수식은 각각의 volume pair를 optimize해야하며, 많은 volumes를 registering하는데 많은 비용이 소모됨

이와 같은 한계 해결을 위해 Guha Balakrishnan et al.은
1) 사용 데이터에 대한 registration field가 계산될 수 있다고 가정하며,
2)  데이터세트의 예상 energy를 최소화하는 방향으로 function parameter를 optimize함
     (pair 별 optimization → global optimization으로 대체, ※amortization이라고도 부름)

global function으로 추정 ▶ 주어진 volume pair에 대한 함수를 평가하여 필드 생성이 가능해 속도 향상 가능

 

 

Related Work

ⓐ Non-Learning 기반의 Medical Image Registration
       1) Diffeomorphic Distance Metric Mapping (LDDMM)
       2) DARTEL
       3) Diffeomorphic demons
       4) Standard Symmetric Normalization (SyN)

    - Non-learning 기반의 registration기법들은 모두 변위벡터변환(Displacement vector field)을 위한 기법으로
      energy function을 기반으로 하는 느린 registration 기법들임
      (GPU 사용 시 속도를 줄일 수 있지만 registration 작업 때마다 GPU를 사용해야 한다는 문제점 존재)
    

ⓑ Learning 기반의 Medical Image Registration

    - 대부분의 learning 기반 registration 기법은 지도학습(supervised learning)에 의존한 기법들임
       (deformation simulating, 각 pair에 대한 전통적인 registration방식을 learning, 유사도 측정으로 field 도출)

1) X. Cao et al., "Deformable image registration based on similarity-steered CNN regression", 
Proc. Int. Conf. Med. Image Comput. Comput.-Assist. Intervent, pp. 300-308, 2017.

2) J. Krebs et al., "Robust non-rigid registration through agent-based action learning", 
Proc. Int. Conf. Med. Image Comput. Comput.-Assist. Intervent. (MICCAI), pp. 344-352, 2017.

3) M.-M. Rohé, M. Datar, T. Heimann, M. Sermesant and X. Pennec, "SVF-NET: Learning deformable image registration using shape matching", Proc. Int. Conf. Med. Image Comput. Comput.-Assist. Intervent. (MICCAI)
, pp. 266-274, 2017.

4) H. Sokooti, B. de Vos, F. Berendsen, B. P. Lelieveldt, I. Išgum and M. Staring, "Nonrigid image registration using multi-scale 3d convolutional neural networks", Proc. Int. Conf. Med. Image Comput. Comput.-Assist. Intervent. (MICCAI), pp. 232-239, 2017.

5) X. Yang, R. Kwitt, M. Styner and M. Niethammer, "Quicksilver: Fast predictive image registration—A deep learning approach", NeuroImage, vol. 158, pp. 378-396, Sep. 2017.

    - supervised learning 방식은 정립되고 검증된 방향으로 학습방향을 제시함
      하지만 label 데이터를 획득하기 어려울 수 있고, 새롭게 변형되는 유형에 대해 대처하지 못함

    - 기존에 존재하던 Unsupervised learning 방식들은 모두 CNN을 통해 공간적인 변형(spatial transformation)을 진행함
       하지만 이러한 방식들은 제한된 volume(e.g., 2D slice, 3D의 subregions)에 대해서만 사용될 수 있으며,
       대규모의 transformation이 불가능함
      ※ Voxel Morph는 unsupervised learning의 한계를 개선하기 위해 다음과 같은 분석을 진행함
          1) 다양한 label에 대한 가용성이 overall한 registration에 어떤 성능을 미치는지 평가
          2) 다양한 시나리오에서 유사도 함수의 loss 및 정규화 함수의 loss 조합이 어떻게 작동하는지 평가

 

 

 

Method (Voxel Morph)

VoxelMorph는 3차원 영상을 중심으로 설명하지만, 다른 차원도 똑같은 이론으로 적용가능함.
VoxelMorph 모델에 사용되는 데이터셋은 affine 변환으로 preprocessing 하였으며, non-linear한 misalignment volume만 남아있는 상태에서 실험 진행

Overview of VoxelMorph

 

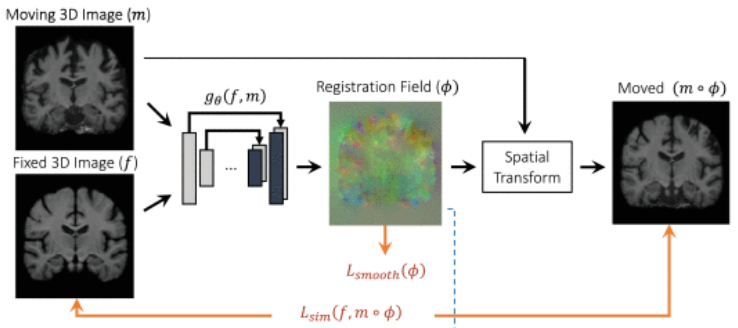
Guha Balakrishnan et al.은 CNN을 기반으로 gθ(f,m)을 고안하며, 이를 u라고 표기함

θ: convolution layer의 커널로 network parameter

 

u를 통한 학습방식

n차원의 데이터에서 f와 m 사이의 displacement field u는 n+1 차원의 이미지에서 실질적으로 저장되며,
각각의 voxel을 p라고 가정할때, u(p)는 f(p)와  [m∘ϕ](p)간의 위치적 유사성을 향상시키는 방향으로 학습함
(u를 통해 최종적으로 도출된 ϕ은 registration을 위한 field map)

ϕ=Id+u (u를 identity transform)

 

학습에 사용한 모델

CNN기반의 모델로 구성하였으며, encoder와 decoder, skip-connection 기반으로 하는 U-Net을 활용함

convolution layer: 계층적(hierarchical feature) 분석
encoder: 공간차원 축소를 위해 사용(input의 거친 표면에 대해 분석하기 위해)
decoder: encoder에서 얻은 정보를 그대로 registration에 사용하기 위함

 

Lsim & Lsmooth 학습

 

제안하는 unsupervised loss 수식

 

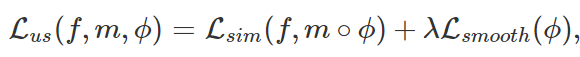
VoxelMorph는 기존의 energy function과 동일한 loss function을 위와 같이 활용함

Energy function과 동일하게 Lsim(유사성)과 Lsmooth(정규화) 함수를 사용하지만, m ∘ ϕ 계산방식에서 차이를 둠

m ∘ ϕ 계산방식은 다음 수식과 같음

 

m ∘ ϕ 계산방식

 

 

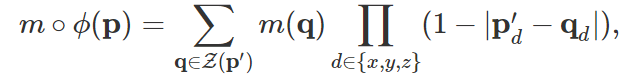
m = moving
p = 각각의 voxel
p' = p+u(p) ( 선형보간된 p 위치, p는 정수형으로 위치되어 있어 이웃 voxels를 통한 선형 보간 필요)
Z(p') = voxel neighbors (선형보간된 p'의 이웃voxel모음)
q = p'의 이웃voxel
d = dimension(차원)

 

 

moving의 각 voxel은 이웃 voxel들을 통해 linear interpolation되며, 이 값들은 각 차원별로 구분되어 Lsim 함수의 값을 도출하는데 사용됨

 Voxel Morph에서는 Lsim 계산을 위해 ① MSE(Mean Squared Error) ② CC(Cross-Correlation) 방식을 활용함 

 

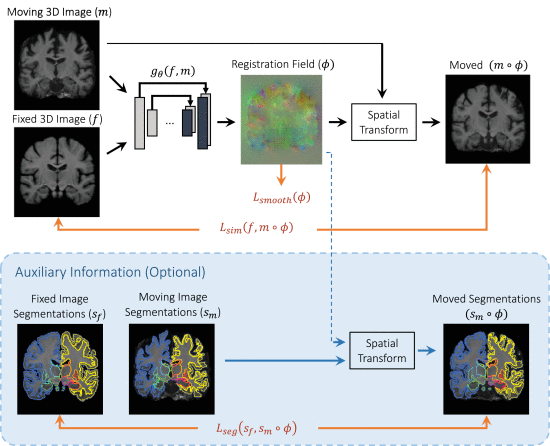
Auxiliary Data Loss Function (segmentation 보조학습)

 

Auxiliary Information Training

 

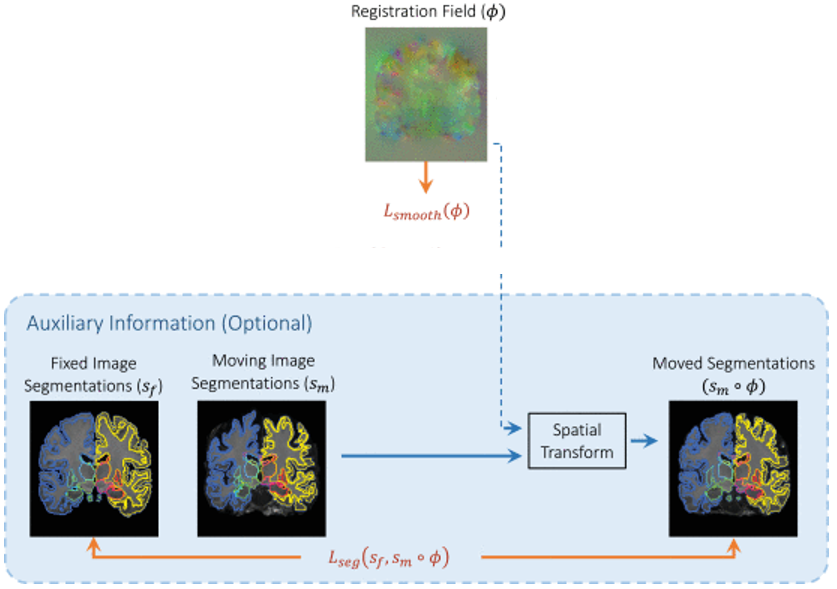
Registration field는 각 voxel의 해부학적 구조를 표현할 수 있어 Segmentation 훈련과정에 사용될 수 있음

Registration field가 좋은 학습으로 잘 추출이 됐다면 fixed인 f와 m∘ϕ는 overlap시 해부학적으로 동일한 구조가 되어야 함

 

∴ f와 m∘ϕ에 대한 voxel들을 이용하여 Dice score를 구하는 방식으로 segmetation 학습을 할 수 있으며 수식은 다음과 같음

Segmentation loss function

Dice Score of Voxel Morph

 

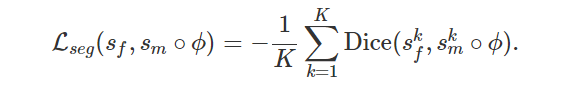
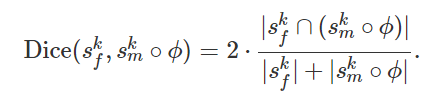
k: voxels structure

 

Auxiliary learning을 위해서는 다음과 같은 loss function을 추가해 학습함

 

Auxiliay learning을 포함한 loss function

 

 

 

 

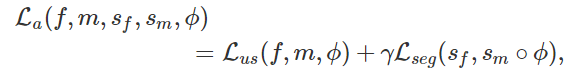
Experiments

 

실험환경

1) Dataset
    OASIS, ABIDE, ADHD200, MCIC, PPMI, HABS, Harvard GSP, FreeSurfer Vuckner40(Un-seen data)
    (획득경로, 연령 및 건강상태는 dataset마다 상이하며, 모든 data는 256x256x256 voxel 사이즈로 resampling)

2) Pre-processing
    ① Linear한 misalignment volume 제거를 위해 Affine 변환 사용 (FreeSurfer로 affine 변환)

    ② Crop (160x192x224)

 

3) Data Split
    Train:Val:Test = 3231:250:250 (Volume)

 

4) Evaluation Metrics

     Dice Score(segmentation 성능검증),  Jacobian matrix(regularity 성능 검증)

 

5) Voxel Morph Training
    Tensorflow, Keras, ADAM Optimizer, Learning rate: 0.0001, Mini-batch SGD, Iteration: 150,000

    

※ 모든 실험과정에서 supervision정보는 사용하지 않음 (supervised learning 방지)

 

 

실험조건

실험은 6가지 조건으로 진행함

 

1) Registration 성능분석

2) Hyper-parameter sensitivity 분석

3) training set 크기에 따른 registration 영향력 분석

4) Annotation 자동화 성능 분석

5) Unseen data에 대한 test결과 분석

6) Auxiliary segmentation을 추가한 registration 분석

 

 

 

1) Registration 성능분석

Registration 성능

 

ⓐ Base-line으로 꼽히는 SyN과 Nifty Reg에 비해 향상된 dice score를 보임 (0.753)

ⓑ Deffeomorphic 변형 평가를 위한 Jacobian matrix는 모두 1%미만의 수치를 보여 자연스러운   
     smoothing(regularization)이 이루어졌음

ⓒ CPU연산시간을 획기적으로 줄임 (9059sec → 57sec)

Deffeomorphic 변형: 비물리적인 변형(e.g., 구조 뒤집힘)이 있는 변형으로, 비정상적인 변형을 의미함
                                  (※의료영상 분석 분야에서의 deffeomorphic변형은 비정상적인 변형이나 손상으로 간주해
                                  주의깊게 분석해야함)
                                  ∴ Jacobian 행렬식이 0 이하인 voxel은 deffeomorphic 변형으로 간주 
                                     ▶ 적을수록 비자연스러운 변형이 적게 일어났음을 의미

양수가 아닌 Jacobian 행렬식의 voxel수 (Table 3열)
 -   520만개의 전체 voxel 중  3열의 voxel만큼 비자연스러운 변형이 일어났음

 

양수가 아닌 Jacobian 행렬식의 voxel 비율 (Table 4열)
 -  520만개의 전체 voxel 중  4열의 voxel 비율만큼  비자연스러운 변형이 일어났음 (실험결과 모두 1% 미만)
    ▶  전체 voxel 중 비자연스러운 변형이 일어난 voxel은 매우 적음을 의미함
          하지만, 매우 소수(1%미만) 의 경우 비정상적인 변형이 발생했음

 

 

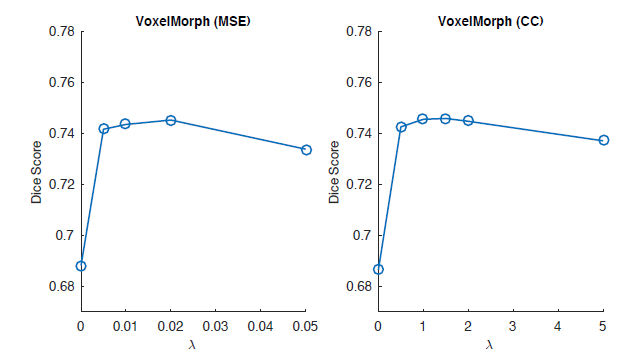
2) Hyper-parameter sensitivity 분석

 

Validation set의 Voxel Morph dice score

 

 

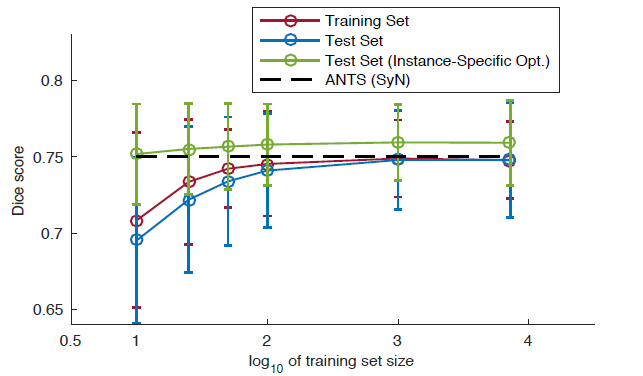
3) training set 크기에 따른 registration 영향력 분석

 

Training set에 따른 dice score

 

 

4) Annotation 자동화 성능 분석

 

Dice Score of Manual Annotation

 

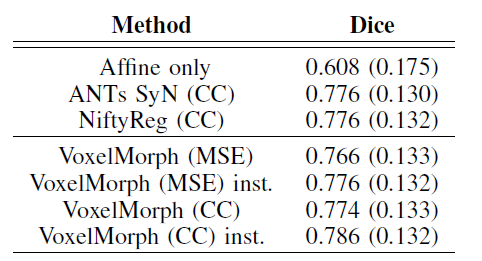
Un-seen Data(Buckner40)에 대해 annotation성능을 분석, base-line과 비슷하거나 향상된 성능을 보임

inst. : instance-optimization(추가적인 인스턴스 최적화 과정)

 

 

5) Unseen data에 대한 test결과 분석

 

 

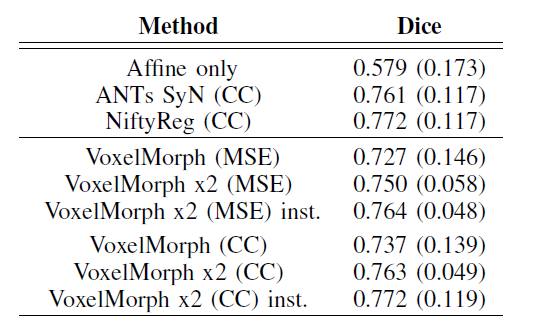
CC(Cross-Correlation)이 MSE보다 높은 성능을 보임

 

 

6) Auxiliary segmentation을 추가한 registration 분석

 

 

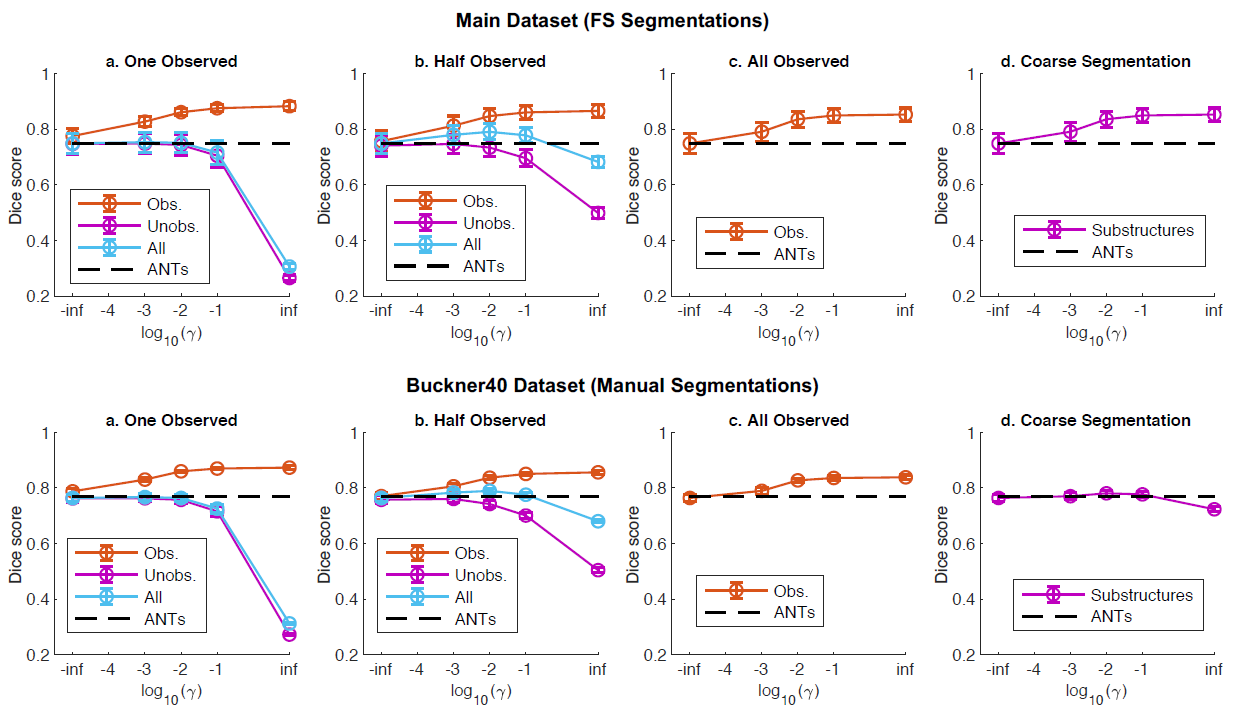
-inf: Auxiliary learning X
inf: Auxiliary label 만 학습에 사용 (smoothness나 이미지 교정 x)
a: One Obseved: 30개의 뇌 세부 구조 중 1개의 구조만 auxiliary learning
                        (대표적 구조인 hippocampi, cerebral cortex, cerebral white matter, ventricles구조를 사용,
                         각 결과는 K-fold로 평균)
b: Half Observed: 30개의 뇌 세부 구조 중 15개의 구조만 auxiliary learning
c: All Observed: 30개의 뇌 세부 구조를 모두 auxiliary learning
d: Coarse Segmentation: 더욱 세세한 segmentation에서의 auxiliary learning 성능 비교
    (e.g., white matter, gray matter, cerebral spinal fluid는 각각 다른 구성요소이지만 segmentation 시
     white matter로 뭉뚱그려 처리하는 경우가 많음, 이러한 한계를 개선하기 위해 auxiliary learning으로
     더욱 세부적인 학습이 가능함)

 

 

Discussion & Conclusion

Voxel Morph의 차별점

◎ Un-supervised learning 방식에서 base-line방식과 비슷한 성능을 도출하면서 가장 빠른 연산속도

◎ 기존의 registration은 pair별 최적화를 진행하지만, voxel morph는 gθ(⋅,⋅)함수를 통해 전역(global) 최적화를 진행함
    ▶범용적이고 자연스러운 최적화 가능(데이터 유연성 확대, 대량 데이터셋 필요X)

◎ Auxiliary learning을 통해 세부적인 segmentation training 가능
    ▶Segmentation 성능 향상