https://arxiv.org/abs/2103.13630
Low-power Computer Vision, 2022
A Survey of Quantization Methods for Efficient Neural Network Inferenc
This chapter provides approaches to the problem of quantizing the numerical values in deep Neural Network computations, covering the advantages/disadvantages of
www.taylorfrancis.com
Abstract
AI분야에서 신경망 모델의 성능발전으로 인해 메모리 및 computational resource 관련 한계가 발생하고 있음.
해당 한계를 개선하기 위한 optimization기법을 다루며, 특히 quantization에 대한 다양한 접근 방식을 조사함.
Introuduction
- Neural Architecture Search (NAS)
특정 하드웨어 플랫폼에 맞게 NN architecture를 설계하는 것.
NN 구성요소의 오버헤드가 하드웨어에 따라 달라지기 때문에 architecture의 설계가 중요 - Pruning (가지치기)
민감도가 작은(모델 output 및 loss function에 영향이 없는) 뉴런을 제거함으로써 희소행렬을 생성.
Pruning은 Unstructured pruning과 Structured pruning으로 구분됨.
Unstructured pruning : 모델의 generalization에 거의 영향을 주지 않으면서 대부분의 parameter를 제거 가능
속도가 느리고 , 메모리에 바인딩되는 희소행렬 작업으로 수행됨
Structured pruning : 파라미터 그룹(ex. 전체 convolutional filter)이 제거함으로써 pruning,
정확도가 크게 저하되는 경우가 생길 수 있으며,
성능을 유지하며 높은 수준의 가지치기를 하는 방식은 아직 해결되지 않음. - Knowledge Distillation (지식증류)
대규모 모델(teacher model)을 훈련한 뒤 이를 경량화된 모델(student model)에 전이시키는 방식
teacher model이 student model을 학습시킬 때 hard-label을 사용하는 대신 soft-label을 활용하여 지식의 전이를 효과적으로 진행함. 지식증류는 높은 압축비를 달성하지만 정확도가 저하되는 경향이 존재함. 하지만 지식증류와 다른 최적화 방식(ex. pruning, quantization)과 결합하여 사용 시 매우 효과적임 - Quantization (양자화)
NN모델의 training과 inference에서 모두 일관된 성공을 보여준 방식으로, 본 논문에서는 inference에 대한 quantization에 초점을 맞추고 있지만. training에서도 매우 좋은 성능을 보임.
특히, half-precision과 mixed-precision training은 AI모델이 훨씬 더 높은 처리를 가능하게 함.
하지만 half-precision(반정밀도) 이상의 경량화는 매우 어려운 것으로 입증되었으며, 최근 quantization 연구의 대부분은 inference에 중점을 두어 진행 중임. - Quantization & Neuroscience(양자화와 신경과학)
신경과학분야에서 인간의 두뇌는 연속적인 형태가 아닌 이산적인 형태로 정보를 저장될 수 있음
(연속적인 형태로 저장되나 noise(열, 외부, 시냅스 소음)등에 의해 손상됨)
이산적인 정보는 이러한 noise에 더 강력하며, 더 높은 일반화 능력을 가질 수 있음. 또한, 제한된 자원환경에서 더 높은 효율성을 가질 수 있어 Qunatization과 neuroscience는 연관되어 있음.
General History of Quantization
Quantization은 미적분학(최소 제곱법)에서 부터 적분 계산의 근사화까지 1800년대 초반부터 이루어진 연구분야임.
최근에는 신호를 디지털 형식으로 표현하기 때문에 디지털 신호처리에서 양자화가 매우 중요해짐.
1948년 Shannon은 디지털 컴퓨터에서의 양자화 효과 및 양자화 사용이 처음으로 제안됨. Shannon은 사건의 확률에 따라 bit를 변경하는 Variable-Rate Quantization(가변율 양자화)를 제안하며, 이 기법을 기반으로 허프만 코딩이 제안됨.
이러한 연구를 바탕으로 distortion-rate quantization, pulse code modulation(PCM)등이 연구됨.
Quantization in Neural Nets
NN모델에서 quantization이 중요한 이유는 다음과 같음.
1) neural net의 inference와 training은 모두 계산 집약적임 => 수치를 효율적으로 표현하는 것이 매우 중요
2) 대부분의 NN모델은 과도하게 paramerized되어 있으며 정확도에 영향을 주지않고 충분히 bit precision을 줄일 수 있음
NN모델은 quantization에 매우 robust(성능 ↑) 하지만, NN의 상용화(application)을 위해 잘 해결된 연구가 없음
NN의 quantization에는 exact(정확성)와 discretized(이산화) 사이의 차이를 제어하는 연구가 많이 진행되었으며, 특히 신경망의 서로 다른 레이어는 손실함수에 서로 다른 영향을 미친다는 연구결과가 quantization에 대한 연구에 동기를 부여했음.
Basic Concepts of Quantization
Basic Quantization은 다음과 같이 구분됨.
A) Uniform Quantization & Non-Uniform Quantization
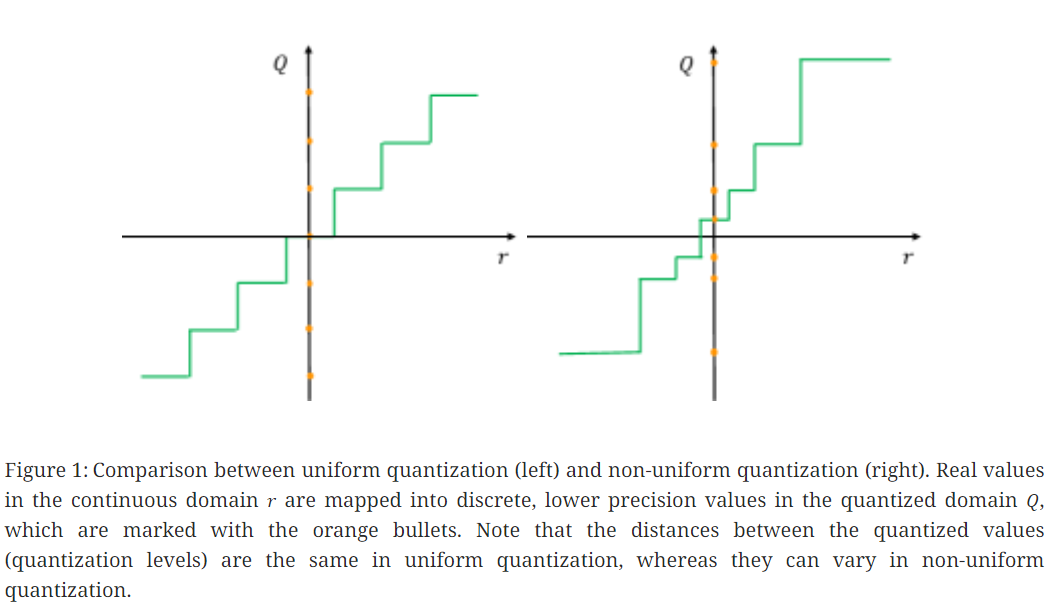
(1) Uniform Quantization
Uniform quantization은 모든 quantized 값의 구간이 같은 크기를 가짐
대중적인 quantization function은 다음과 같음
$$Q(r) = Int\left ( r/s \right )-Z$$
Q는 quantizaiton operator이며, $Z$는 정수형태의 zero point를 의미함. 여기서 int함수는 반올림을 통해 실수값을 정수형 값으로 매핑하는 역할을 함. $r$은 real value를 의미하고, 이러한 quantization기법을 uniform quantization이라고 하며,
이는 figure 1의 왼쪽그림과 같음.
(2) Non-Uniform Quantization
Uniform Quantization과 달리 Non-uniform Quantization에서의 quantization level은 불균일한 간격으로 이루어지며,
figure 1의 오른쪽 그림과 같이 Non-Uniform 한 quantization의 수식은 다음과 같음.
$$Q(r)=X_{i}, if r \in \left [ \Delta_{i},\Delta_{i+1} \right )$$
$ X_{i}$는 discrete quantization level을 의미하며, real value인 $r$은 $\Delta_{i}와 $\Delta_{i+1}$ 사이의 값들로 변형됨.
Non-uniform quantization은 중요한 영역에 더 집중하거나 적절한 동적 범위를 찾아 분포를 잘 포착할 수 있기 때문에 고정된 비트폭에 대해 더 높은 정확도를 보일 수 있음. 많은 Non-uniform quantization방식들은 종모양의 분포로 설계되었으며,
일반적인 rule base 기반의 non-uniform quantization은 로그 분포를 통해 설계됨.
일반적으로 Non-uniform Quantization이 parameter 범위를 불균일하게 구분함으로써 정보를 더 잘 파악할 수 있는 방법이나, 일반적인 gpu 및 cpu환경에서 효율적으로 배포되기 어려움. 따라서, non-uniform quantization보다 uniform quantization이 하드웨어에 대한 효율적인 매핑으로 구분되어 많이 쓰임.
B) Symmetric & Asymmetric Quantization
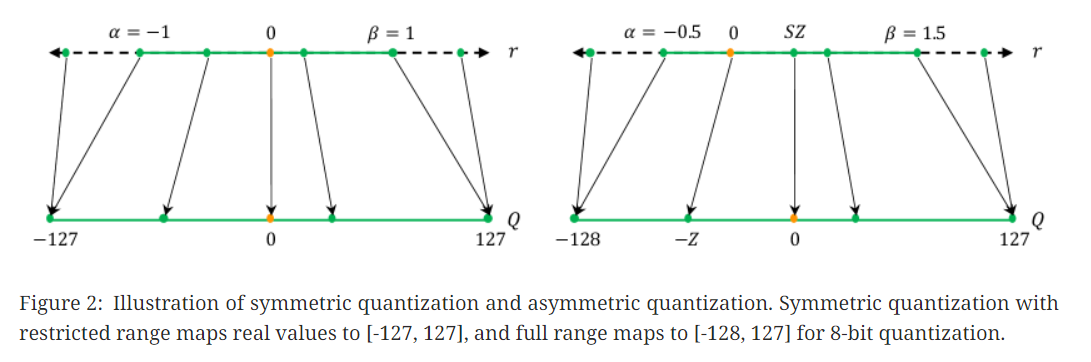
(1) Symmetric Quantization
Symmetric Quantization은 zero-point(영점)이 입력값 범위의 중앙에 위치하도록 설정하며 figure2의 왼쪽 그림과 같음.
Symmetirc quantization은 Uniform quantization에 속하며, 주로 변환할 데이터의 절대값이 대칭적인 분포를 가질 때 유용함.
Uniform quantization에서 가장 중요한 요소는 scaling factor인 S를 정하는 것임.(Uniform Quantization 수식에서)
S를 구하는 것을 Calibration이라고 하며, 수식은 다음과 같음.
$$S = \frac{\beta -\alpha }{2^{b}-1}$$
여기서, $\alpha$는 $r_{min}$을 의미하며, $\beta$는 $r_{max}$를 의미함.
위 식에서 symmetric quantization이 되기 위한 조건은 $\alpha = - \beta$임
(2) Asymmetric Quantization
Asymmetric quantization은 symmetric quantization과 반대로 $\alpha != - \beta$인 불균형한 분포를 quantized하는 방식임. Asymmetric quantization을 하는 경우는 weight나 activation function값이 불균형할 때 쓰임(e.g., ReLu)
일반적으로 Non-uniform Quantization이 parameter 범위를 불균일하게 구분함으로써 정보를 더 잘 파악할 수 있는 방법이나, 일반적인 gpu 및 cpu환경에서 효율적으로 배포되기 어려움. 따라서, non-uniform quantization보다 uniform quantization이 하드웨어에 대한 효율적인 매핑으로 구분되어 많이 쓰임.
Symmetric & Asymmetric Quantization은 모두 널리 사용되는 방식임. 하지만 이러한 접근 방식은 activation function에서의 outlier에 매우 취약함 (범위가 불필요하게 증가하며, 양자화 성능이 떨어질 수 있기 때문)
이러한 문제를 해결하기 위해 최소/최대값을 사용하는 대신 다음과 같은 방식을 사용할 수 있음.
1) 백분위 사용 (i번째 최소,최대값을 선정)
2) real value와 quantized value 간 KL divergence를 통한 최소,최대값 선정
※ Symmetric Quantization ∈ Uniform Quantization
Asymmetric Quantization은 Uniform, Non-Uniform에 속할수도 있고 안속할수도 있음 (flexible)
C) Static & Dynamic Quantization
Quantization에서 clipping 범위를 결정하기 위한 방식을 위해서 다룸. 이 섹션에서는 clipping 범위를 결정하는 시점에 대해 다룸.
(1) Static Quantization
Static quantization은 inference 전 clipping 범위를 미리 계산하여 고정하는 방식임.(e.g., weight가 고정되어 있는 경우 활용)
이 기법은 미리 계산과정을 거치기 때문에 inference에서 추가적인 계산 overhead는 없지만, dynamic quantization에 비해 모델 성능이 감소할 수 있음.
Static quantization에서 가장 대표적인 방법은 activation의 전형적인 범위 계산을 위해 clibration input series(보정된 입력 묶음)을 활용하는 것임. 또한, MSE, entropy등도 활용가능하며, NN모델 training 시에 clipping 범위를 학습하거나 적용하는 방식도 존재함.
(2) Dynamic Quantization
Dynamic quantization은 inference 동안 각 activation map마다 동적으로 계산됨. 이러한 방식은 실시간으로 최소값, 최대값, 백분위 등과 같은 값을 계산해야 하기때문에 추가적인 overhead가 발생함.( ∴ inference 시간의 절감효과 떨이짐)
하지만, 각 input에 대해 clipping 범위를 정확하게 계산하기 때문에 성능을 유지할 수 있으며, 종종 더 높은 성능을 달성하기도 함.
Dynamic quantization은 좋은 성능을 가지지만 static quantization보다 시간적 비용이 많이 소요됨.
따라서, 실무적으로는 모든 input에 대해 clipping 범위가 고정되는 static quantization을 주로 사용함.
D) Quantization Granularity
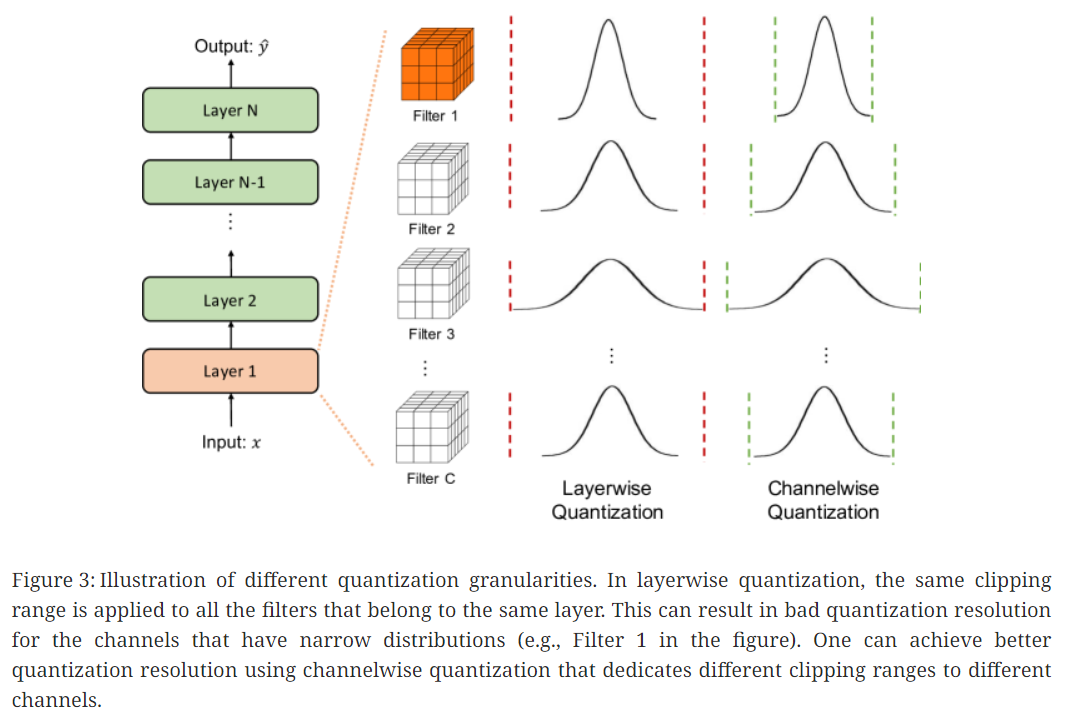
대부분의 computer vision분야에서 layer의 activation input은 figure 3과 같이 다양한 convolution filter로 convolution됨. 따라서, 이러한 각 convolution filter값들은 모두 다른 범위를 가짐. 이러한 이유로 quantization 시 clipping 범위가 얼마나 잘 세분화 되어 있는지 또한 중요한 요소임.
Clipping범위를 세분화하기 위한 방식들은 다음과 같음
(1) Layerwise Quantization
Layerwise quantization은 각 layer별로 가진 통계적 분포를 고려해 최적의 clipping범위를 결정함.
같은 layer 내에서는 모든 convolutional filter에 대해 동일한 clipping 범위를 사용하기 때문에 구현하기 간단하지만 정확도가 최적이 아닐 수 있음. (각 convolution filter간 범위가 다를 수 있기 때문)
(2) Groupwise Quantization
activation 값이나 convolution kernel의 clipping 범위를 계산하기 위해 layer 내부에서 여러개의 채널로 범위를 그룹화하는 방식. 이는 convolution이나 activation의 분포가 많이 달라지는경우에도 도움이 될 수 있음 (e.g., attention layer로 연결된 transformer). 하지만, 다양한 스케일링 요소를 고려해야 하기 때문에 추가 연산비용이 발생함.
(3) Channelwise Quantization
가장 대표적인 방식이며, 채널과 독립적으로 각 convolution filter에 대해 고정값을 사용함.
이는 더 나은 quantized resolution을 보장하고 더 좋은 성능을 낼 수 있음.
(4) Sub-channelwise Quantzation
이전까지 제안되었던 방법들은 모두 layer의 paramter그룹에 대해 clipping범위가 결정되는 극단적인 방법임.
이러한 방법들은 다양한 다양한 scaling factors를 고려해야 하기 때문에 상당한 overhead가 발생함.
따라서, quantization resolution과 computation overhead 간의 절충안으로 사용
※ 거의 안씀
E) Fine-tuning Methods
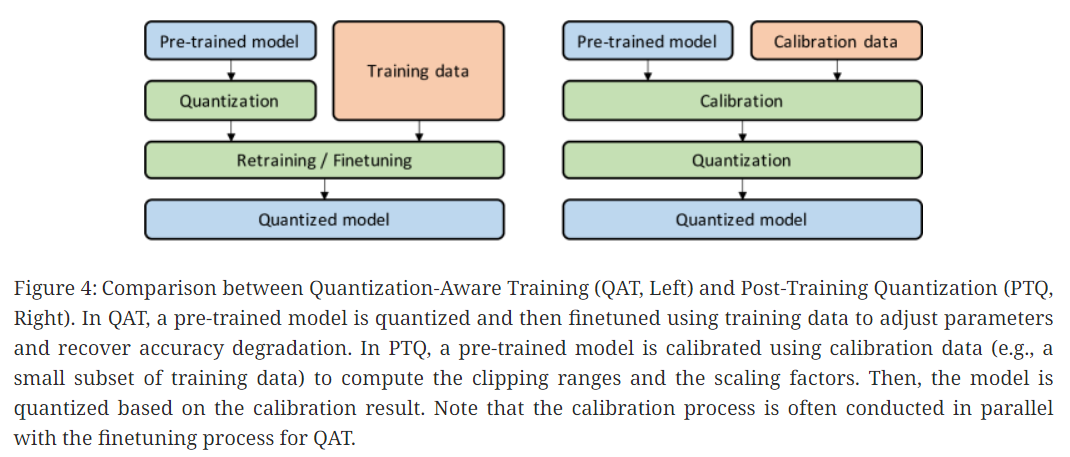
Quantization 후 NN의 parameter를 조정해야 하는 경우가 많음.
Quantiztion 뒤 parameter 조정은 아래 3가지 기법을 통해 가능함.
(1) Quantization-Aware Training (QAT)
Quantized 후 발생된 perturbation으로 인해 수렴지점에서 멀어질 수 있음.
QAT는 모델 재학습을 통해 parameter를 재훈련하는 방식으로 문제를 해결하며, figure4의 왼쪽 그림과 같음.
학습 시 forward propagation 및 backpropagation시 부동소수점으로 수행되는 일반적인 학습과 달리 QAT는 각 gradient update 뒤 parameter를 quantization함. (quantization 후 gradient를 update하면 zero-gradient나 high error가 있는 gradient를 가질 수 있기 때문)
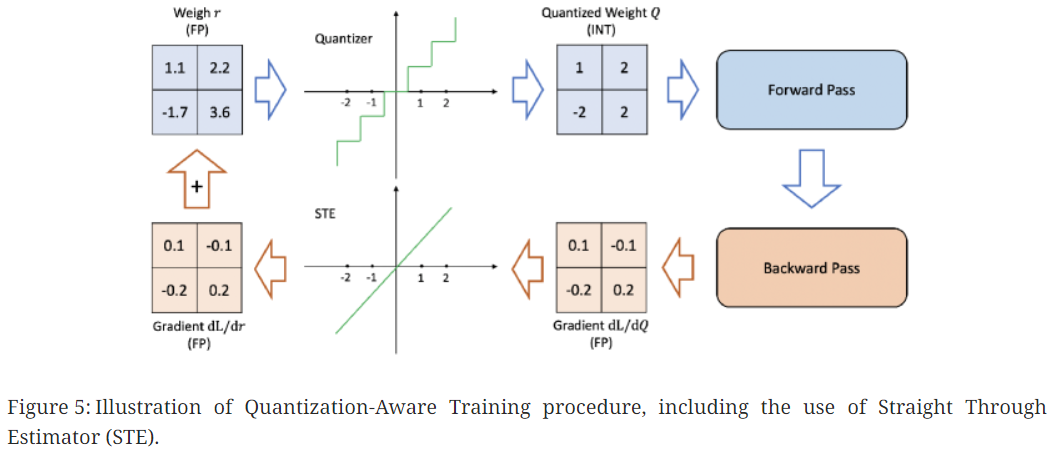
QAT에서 중요한 부분은 back-propagation에서 비분 불가능한 연산자가 처리되는 방식임.
Figure 5의 윗쪽 graph를 보면 quantization으로 인해 거의 모든 곳에서 기울기가 0인것을 확인할 수 있음.
이러한 문제를 해결하기 위한 대표적 방안은 STE(Straight Through Estimator)임.
STE(Straight Through Estimator) : 반올림연산을 무시하고 figure 5의 아래 graph처럼 항등함수(identity function)을 사용하여 근사하는 방식
STE의 대략적인 근사에도 불구하고 binary quantization이나 초정밀 양자화(ultra low-precision quantization)을 제외하고는 모든 모델에서 잘 작동함. STE가 아닌 여러 방식도 제안되었으나, 조정이 많이 필요한 이유로 지금까지 STE 접근방식이 가장 일반적으로 사용됨.
QAT는 STE를 통해 잘 작동하는 방식이나, NN을 재학습시키기 때문에 계산비용이 추가적으로 발생한다는 단점이 있음. 특히, low-bit precision quantization 시 성능을 복구하기 위해 수백번의 epoch를 수행해야 할 수도 있음.
하지만, quantized된 모델이 장기간 배포될 예정이고 효율성과 정확성이 중요하다면 사용할 가치가 있음.
(2) Post-Training Quantization (PTQ)
비용적 한계가 있는 QAT의 대안은 weight에 대한 미세조정이나 fine-tuning이 필요없는 post-training quantization(PTQ)임.
PTQ의 overhead는 매우 낮아 무시할 수 있을 정도이며, 훈련을위한 훈련데이터가 필요없어 데이터가 제한적이거나 label이 지정되지 않은 상황에서 적용할 수 있음. 하지만, low-precision quantization 시 QAT에 비해 성능이 떨어짐.
따라서, PTQ의 성능 저하를 완화하기 위해 다양한 접근 방식이 제안됨. (e.g., quantization에 따른 weight 평균 및 분산의 편향을 보정, 서로 다른 layer나 channel 간 weight 범위를 균등화)
(3) Zero-shot Quantization
Quantization 후 성능저하를 최소화하기 위해서는 calibration 및 fine-tuning을 진행해야 하며, 훈련데이터에 대한 접근이 가능해야 함. 하지만 대부분의 quantization 과정에서는 원래의 훈련데이터에 접근하기 매우 어려움 ( ∵ 대용량의 데이터셋, 의료 데이터셋 )
이러한 문제를 해결하기 위한 방안이 zero-shot quantization(ZSQ)이 있으며, 본 논문에서는 2개의 level의 zero-shot quantization을 설명함.
- Level 1 : Data X, Finetuning X (ZSQ + PTQ)
- Level 2 : Data X, Finetuning O (ZSQ + QAT)
Level 1의 경우 매우 빠르고 간편하지만 성능적으로 우수하지 못함.
Level 2의 경우가 가장 많이 활용되는데, level 2에서 활성화된 연구분야는 pre-trained model에서 실제 훈련데이터와 유사한 합성데이터를 생성하는 것임.
합성 데이터 생성을 위해서 generative adversarial network(GAN)이 활용될 수 있으며, 합성된 데이터를 사용하여 fine-tuning이 가능함. 그러나 이 방식은 모델의 내부 통계를 고려하지 못하기 때문에 생성된 합성 데이터가 실제 데이터 분포를 제대로 나타내지 못할 수 있음. 이러한 한계를 해결하기 위해 batch normalization에 저장된 통계 (channel별 평균이나 분산)을 사용해 실제 데이터에 가까운 합성 데이터를 생성하는 연구도 진행되고 있음. 또한, 내부 통계의 KL divergence 발산을 최소화하여 데이터를 생성하는 연구도 진행 중임. 이러한 방식들을 통해 실제 훈련/검증 데이터에 접근하지 않고도 정확한 quantization이 가능함.
Zero-shot Quantization은 데이터셋 접근 없이 고객에 모델을 배포하는 서비스에서 특히 중요함. 또한, 보안이나 개인정보 보호문제로 인해 데이터셋 접근이 어려운 경우에도 유용하게 사용될 수 있음.



