[CVPR2023] Adaptive Data-Free Quantization

 

https://openaccess.thecvf.com/content/CVPR2023/html/Qian_Adaptive_Data-Free_Quantization_CVPR_2023_paper.html

 

Abstract
Data Free Quantization에서 Quantized Model의 성능을 복원하기 위해 가짜의 데이터 샘플을 생성하는 경우가 많음.
하지만, 기존 방식은 양자화가 진행되지 않은 Full-precision Model P을 기준으로 생성되기 때문에 Quantized Model과는 독립적이며, 생성된 샘플이 Quantized Model에 효과적인지 검증되지 않음. 또한, 일반화 오류가 존재해 다양한 Quantization 비트 폭에서 적응성이 좋은지 밝혀지지 않음.

(Quantization은 32bit에서 3,4,5 bit 등으로 compression 강도를 조절해 경량화)
본 논문에서는 이러한 점을 밝히기 위해 Adaptive Data-Free Quantization(AdaDFQ)라는 방식을 제안함.
AdaDFQ는 생성기 G와 양자화 네트워크 Q 간에 제로섬 게임의 관점을 적용하여 샘플 적응성을 강화시킴.

제로섬게임: 게임에 참가한 모든 참가자들의 점수를 합산했을때 총합이 항상 0인 상태

 

AdaDFQ를 통해 새롭게 제안하는 내용은 다음과 같으며, Zero-shot Quantization분야에서 SOTA를 달성함.
1) 적응성이 큰 경우 Q의 일반화에 도움이 되는 샘플 생성에 좋지않음

2) 생성된 샘플은 Q에만 유익해서는 안되며, P에 대한 정보와도 관련이 있어야 함

 

 

Introduction
생성기 G의 용량을 감안할 때 생성된 샘플은 원래의 훈련 데이터셋을 완전히 복구할수는 없음. 따라서, 생성된 샘플로부터 얻을 수 있는 지식이 Q의 학습에 도움이 되는지 안되는지 의문이 제기됨.
하지만, Full-precision Model P에 맞추어 생성된 샘플은 Quantization 시 다양한 비트폭에 따라 Q에 도움이 되지 않을 수 있음. 따라서, P의 정보는 제한적으로만 Q의 성능을 복구하는데 활용됨.

 

또한, 낮은 비트 정밀도 (ex. 3bit)에서는 생성된 샘플이 P와 Q의 예측 간 불일치가 발생할 수 있음
(P의 예측결과와 Q의 예측결과가 불일치한것을 의미)

높은 비트 정밀도 (ex. 5bit)에서는 Q가 compression이 적게 되었기 때문에 P와 비슷한 성능을 갖음. 따라서 G에서 생성된 샘플 대부분은 Q가 학습을 하는데 영향이 적을 수 있음. 

 

Figure1의 왼쪽그림을 보면 기존 방식인 GDFQ에서는 3bit환경에서 학습이 잘 진행되지 않는 underfitting문제가 발생한것을 알 수 있으며,  5bit환경의 오른쪽 그림에서는 GDFQ가 overfitting이 발생한 것을 확인할 수 있음.

 

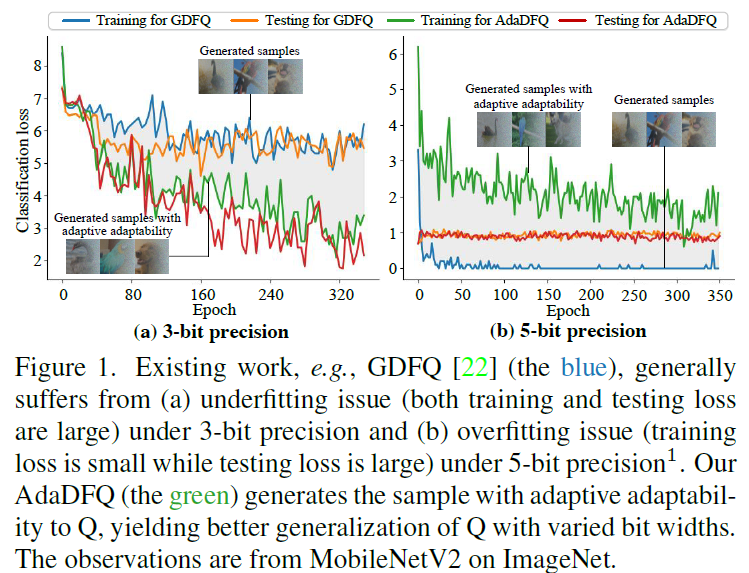
이러한 문제를 해결하기 위해 최초로 제로섬 방식을 사용한 Biao Qian et al.은 adaptability(적응성)을 반영한 데이터 생성방안을 제안함. 하지만 Biao Qian et al.의 방식은 가장 큰 적응성을 가진 샘플이 발생시키는 underfitting 문제를 해결하지 못함.

 

본 논문에서는 이러한 한계를 해결하기 위해 2개 타입의 데이터 샘플을 정의하였음.
1) Agreement Sample (P와 Q가 동일한 prediction)
2) Disagreement Sample (P와 Q가 서로 다른 prediction)

 

위와 같은 데이터 타입을 통해 upper boundary와 lower boundary를 정의하며, 두 boundary안을 margin이라고 정의함.

정의한 margin을 통해 생성되는 데이터의 적응성을 높이며, 다양한 비트폭에서의 활용가능성을 높임.

 

 

Method

 

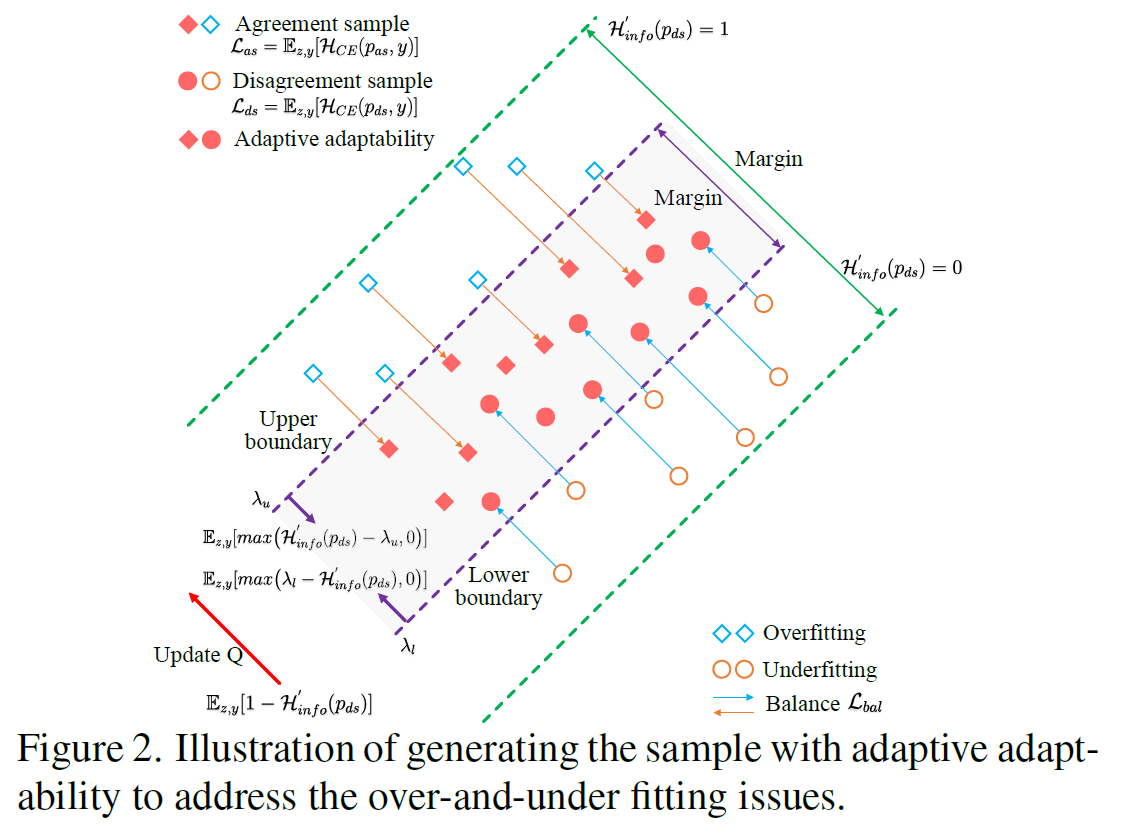
AdaDFQ는 figure2와 같은 구조로 학습됨.

Figure2에서 하늘색의 마름모 point는 agreement sample로 P와 Q가 동일한 예측을 한 샘플을 의미하며,
주황색의 원 point는 P와 Q가 서로 다른 예측을 한 경우를 의미함.

본 논문의 method인 AdaDFQ는 3가지의 주요 과정을 수행함.

1) 제로섬 게임 기반의 적응도 최적화
2) Disagreement sample과 Agreement sample의 균형 조정

3) 2개의 boundary 간 margin 최적화

 

1) 제로섬 게임 기반의 적응도 최적화

Adaptive adaptability를 가진 sample을 생성하기 위해 기존의 제로섬 게임 방식은 아래 수식과 같음.

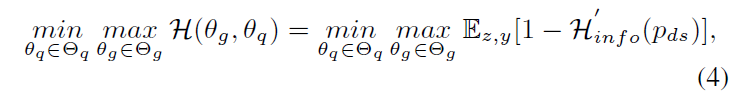
위 수식에서 $H$는 샘플에 대한 적응도를 의미하며, $\theta_{q}$는 quantized model의 parameter, $\theta_{g}$는 generator의 parameter를 의미함.

위 수식을 통해 generator G는 샘플적응도를 최대화시키는 방향으로 학습하는 반면, quantized model Q는 샘플적응도를 최소화하는 방향으로 학습하여 제로섬 게임을 구현함.

하지만, 이러한 방식은 적응도가 매우 큰 샘플에서 underfitting된다는 한계가 있음.
AdaDFQ는 이러한 한계를 분석하고 지적하며, 적응도 향상을 위한 방안으로 agreement sample과 disagreement sample을 정의하고 margin을 활용함.



2) Disagreement sample과 Agreement sample의 균형 조정

Disagreement sample과 agreement sample은 다음과 같은 특성이 존재함.

Agreement Sample 특성
Agreement sample 중 너무 적응성이 뛰어난 몇몇의 샘플들은 특정 비트폭에 특정되어 생성되어 있음. (overfitting)
따라서, 다양한 비트폭에서 효과적으로 사용되지 못할 수 있으며, 이는 일반화 성능의 저하로 전체 성능 또한 저하될 수 있음.

Disagreement Sample 특성
Disagreement sample은 P와 Q가 서로 다른 예측을 하는 underfitting된 샘플을 의미함.
따라서, disagreement sample은 Quantized model Q가 적절한 학습을 할 수 없는 데이터이며, 이러한 샘플을 최대한 줄이는 것을 목표로 해야함.

위 이유들로 agreement sample과 disagreement sample의 적응도와 균형을 조정하여 각 sample들의 단점을 보완할 수 있으며, 각 샘플간의 적응성 조정과정은 다음과 같음.

 

Agreement sample 조정과정
Agreement sample의 overfitting 문제를 해결하기 위해 다양한 비트폭에서도 학습성능이 높아지도록 upper bound 아래 위치한 margin 영역안으로 sample을 조정함. (figure 2 참고)

Disagreement sample 조정과정
disagreement sample은 학습에 도움이 되지 않기 때문에 최대한 줄이되, 존재하는 샘플들은 적응성을 향상시키기 위해 margin 구역 안으로 유도함. (figure 2 참고)

 

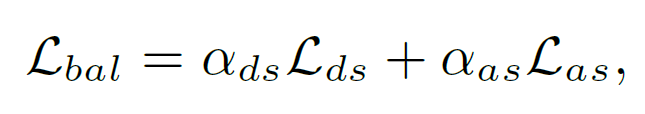
Agreement sample과 disagreement sample간의 균형을 위한 loss는 위와 같이 정의할 수 있음. agreement sample loss인 $L_{as}$에는 $\alpha_{ds}$를 곱함으로써 균형을 조정할 수 있고, 반대의 경우도 동일한 방식으로 균형을 조정할 수 있음.

 

 

3) 2개의 boundary 간 margin 최적화

$L_{bal}$은 margin에 대한 경계가 이상적이어야 적응도를 최대화할 수 있음. 이를 위한 수식은 다음과 같음.

 

여기서 $\beta$는 균형을 위해 사용되며, 적응도정보인 $H$는 upper bound인 $\lambda_{u}$과 lower bound인 $\lambda_{l}$ 사이에 존재함. 

여기서 주요한 부분은 $\lambda_{u}$와 $\lambda_{l}$을 어떻게 정의하는지임.
가장 이상적인 방식은 upper bound와 lower bound가 각 샘플에 대해 각각 개별적으로 정의되는것이지만, 이는 불가능하기 때문에 생성된 모든 샘플에 대한 bound범위를 지정함. 또한, upper bound와 lower bound 값을 0~1 사이로 제한하여 균형을 유지하도록 함.

Experiments

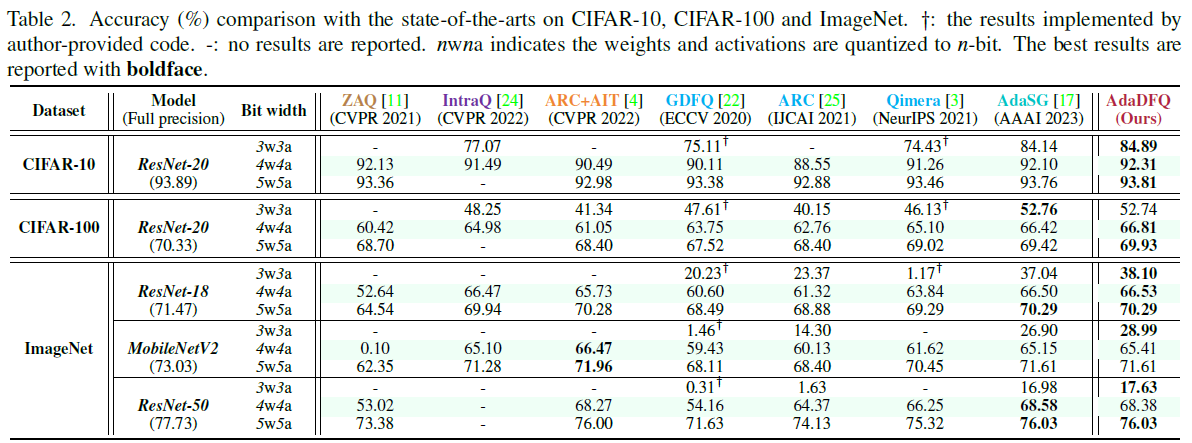
실험결과, 일부 조건을 제외하고 SOTA 성능을 기록함.

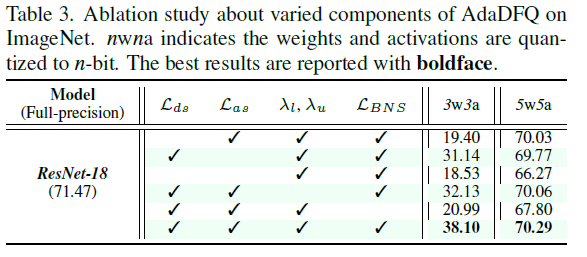
ablation study에서도 agreement sample인 $L_{as}$와 disagreement sample인 $L_{ds}$, upper bound와 lower bound를 모두 사용하였을때 성능이 가장 좋은 것을 확인할 수 있음.

유사도 평가에서도 본 논문에서 제안하는 AdaDFQ는 가장 좋은 성능을 기록하는것을 위 그래프와 표에서 확인할 수 있음.



Conclusion

본 논문에서는 두 플레이어 간 제로섬게임을 활용하는 기존 data free quantization을 재검토하여 적응성을 향상시킴.
Agreement sample과 disagreement sample을 정의하고, 적응도 향상을 위한 upper bound와 lower bound를 추가로 정의하여 두 경계 사이 마진을 최적화하는 AdaDFQ를 제안함

제안방식을 통해 제로섬 게임 활용 시 발생하는 overfitting 문제와 underfitting 문제를 개선하였으며, 두 경계 사이의 adaptive adaptability를 갖춘 샘플을 생성해 Quantized model Q를 효과적으로 보정함. 실험을 통해 Ada DFQ는 기존 방식에 비해 우수한 성능을 입증하였음.